Brilio.net - Penerapan materi dari pelajaran sering kali kita aplikasikan dalam kehidupan sehari-hari. Seperti halnya ketika kamu minum obat sesuai dosis yang diberikan oleh dokter, penggunaan lahan parkir, dan menghitung stok barang dagangan supaya tidak rugi. Kegiatan tersebut adalah penerapan materi matematika loh.
Materi matematika kali ini akan membahas tentang program linear. Dalam pembahasan ini kamu bisa menerapkan materi program linear untuk menghitung keuntungan maksimum dan minimum barang dagangan atau warung orang tua mu. Jika kamu ingin memahaminya lebih detail, bisa simak penjelasan dibawah ini.
Berikut brilio.net rangkum dari berbagai sumber pada Rabu (26/10).
Pengertian program linear
Program linear merupakan suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimum/minimum) diperoleh dari nilai dalam suatu himpunan penyelesaian persoalan dari program linear. Persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear yang akan sering keluar pada soal soal.
Program linear juga merupakan pemecahan masalah dengan menggunakan pertidaksamaan linear. Program linear sebagai bagian dari matematika yang banyak digunakan dalam bidang ekonomi, pertanian, dan perdagangan. Dengan menggunakan program linear, seseorang dapat menghitung keuntungan maksimum atau biaya minimum.
Bagian-bagian program linear
Secara umum, program linear terdiri dari dua bagian diantaranya:
1. Fungsi objektif (fungsi tujuan)
Fungsi objektif adalah fungsi yang nilainya akan dioptimalkan. Fungsi objektif bisa bernilai maksimum atau minimum. Hal ini tergantung pada kasusnya. Bentuk umum fungsi tujuan adalah maksimum atau minimum f(x, y) = px + qy, dengan p dan q adalah konstanta.
2. Fungsi kendala
Fungsi kendala adalah batasan-batasan yang harus dipenuhi oleh peubah yang terdapat dalam fungsi objektif. Bentuk umum dari fungsi kendala adalah sebagai berikut.
ax + by m atau ax + by m
cx + dy n atau cx + dy n
x 0 ; y o atau x 0 ; y o
Karakteristik program linear
1. Program linear dapat mengatasi permasalahan dengan kendala-kendalanya dalam bentuk pertidaksamaan.
2. Program linear dapat mengatasi jumlah kendala yang banyak.
3. Program linear hanya terbatas pada fungsi objektif dan kendala linear.
1-5 Contoh soal program linear beserta pembahasannya [BOLD]
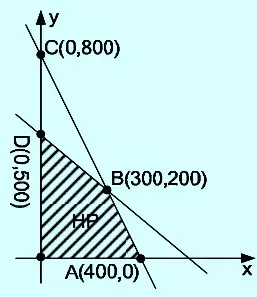
1. Daerah yang diarsir adalah himpunan penyelesaian permasalahan program linear.
foto: soalfismat.com
Nilai maksimum dari z= 40x + 30y adalah...
Pembahasan:
Subtitusi titik (0, 500); (400, 0) dan (300, 200) ke fungsi sasaran z= 40x + 30y sehingga hasilnya sebagai berikut:
~ Z (0, 500) = 40.0 + 30.500 = 15.000
~ Z (400, 0) = 40.40 + 30.0 = 16.000
~ Z (300, 200) = 40.300 + 30.200 = 18.000
Jadi, nilai yang terbesar adalah 18.000 sehingga nilai maksimumnya 18.000.
2. Umur pak Andi 28 tahun lebih tua dari umur Amira. Umur bu Andi 6 tahun lebih muda dari umur pak Andi. Jika jumlah umur pak Andi, bu Andi, dan Amira 119 tahun, maka jumlah umur Amira dan bu Andi adalah...tahun
Misalkan Umur Pak Andi=x, umur Amira=y dan umur Ibu Andi=z
x = 28 + y (1)
z = x 6; atau x=z+6...(2)
x + y + z = 119 (3)
dengan melakukan operasi penjumlahan (1) pada (2) didapatkan
2x = y + z + 34 atau 2x y z = 34...(4)
Lakukan operasi penambahan (3) pada (4) atau
x + y + z = 119
2x y z = 34
3x =153
Atau
x = 51
Dengan melakukan substitusi x pada (1) dan (2) didapatkan
Y = 23; z = 45
Jadi, jumlah umur Amira (y) dan bu Andi (z) adalah y + z = 23 + 45 = 68.
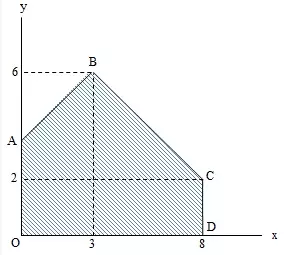
3. Tentukan nilai maksimum fungsi f(x,y)= 4x + 5y yang akan dicapai pada grafik ini!
foto: studiobelajar.com
Pembahasan:
Titik ekstrim pada gambar adalah:
~ A tidak mungkin maksimum karena titik paling kiri.
~ B(3, 6)
~ C(8, 2)
~ D(8, 0)
Nilai tiap titik ekstrim adalah:
B(3, 6) longrightarrow f(3, 6) = 4(3) + 5(6) = 42
C(8, 2) longrightarrow f(8, 2) = 4(8) + 5(2) = 42
D(8, 0) longrightarrow f(8, 0) = 4(8) + 5(0) = 32
Jadi, nilai maksimum ada pada titik yang melalui garis BC dengan nilai maksimum 42.
4. Seorang pemilik toko sepatu ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150 pasang. Toko tersebut hanya dapat menampung 400 pasang sepatu. Keuntungan setiap pasang sepatu laki-laki adalah Rp 10.000,00 dan keuntungan setiap pasang sepatu wanita adalah Rp 5.000,00. Jika banyaknya sepatu laki-laki tidak boleh melebihi 150 pasang, maka tentukanlah keuntungan terbesar yang dapat diperoleh oleh pemilik toko.
Pembahasan :
Pada soal ini, untuk mengetahui keuntungan terbesar maka yang menjadi fungsi tujuan atau fungsi objektifnya adalah keuntungan penjualan sepatu. Jadi fungsi tujuannya adalah :
F(x,y) = 10.000x + 5.000y
Dengan pemisalan :
sepatu laki-laki = x
sepatu perempuan = y
Sistem pertidaksamaan untuk soal tersebut adalah sebagai berikut :
x + y 400
100 x 150
150 y 250
Karena maksimum sepatu laki-laki hanya 150 pasang, maka maksimum sepatu perempuan = 400 150 = 250.
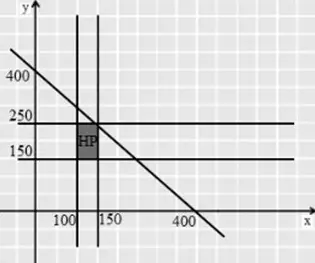
Dari sistem pertidaksamaan tersebut, maka diperoleh grafik sebagai berikut :
foto: soalkimia.com