15 Contoh soal Mean beserta penjelasan, tak perlu khawatir sulit

Brilio.net - Bagaimana cara mencari nilai Mean untuk data tunggal dan kelompok? Simak pembahasan berikut yang disertai dengan contoh soal dan penjelasan.

Dalam dunia Matematika, kamu pasti sering mendengar istilah ukuran pemusatan data. Ukuran pemusatan data yaitu sembarang ukuran yang menunjukkan sejumlah data, namun, sebelumnya telah diurutkan dari data terkecil hingga terbesar atau sebaliknya.

Pengertian Mean.

Mean merupakan nilai rata-rata dari suatu data. Nilai rata-rata ini dihasilkan dari pembagian antara jumlah nilai keseluruhan dengan banyaknya data yang diolah.

Mean atau rata-rata ini biasanya sering dijumpai ketika ingin mengolah suatu data dalam jumlah banyak. Seperti dalam kasus nilai ulangan Matematika di sebuah kelas, dengan jumlah 30 siswa dan dengan nilai yang berbeda-beda. Maka, untuk mengetahui berapa anak yang mendapatkan nilai di atas rata-rata, pasti guru akan mengolah dengan menggunakan rumus Mean.

Macam-macam Mean.

1. Mean data tunggal.

Data tunggal berarti data yang hanya memiliki satu data saja, misalkan 2,4,6,8,10, dst. Dalam menentukan mean data tunggal ini, kamu hanya perlu membagi antara jumlah seluruh nilai dengan banyaknya data yang diolah.

Rumus mean data tunggal.

Mean = (Jumlah semua nilai data) : banyaknya data
x¯¯¯=(x1+x2+...+xn ):n

Cara mencari nilai mean data tunggal.

- Mengurutkan data yang ada mulai data yang terkecil hingga data terbesar
- Jumlahkan masing-masing nilai dari data yang ada secara keseluruhan
- Membagi hasil penjumlahan nilai data itu dengan banyaknya data yang ada.

2. Mean data kelompok.

Data kelompok berarti data yang disajikan memiliki beberapa kelompok interval, dengan jarak tertentu. Misalkan 1-10,11-20,21-30,31-40,41-50.

Dalam menentukan mean atau rata-rata data kelompok ini caranya memang agak sedikit berbeda dengan mean data tunggal.

Rumus mean data kelompok.

Mean = jumlah frekuensi x nilai data : jumlah frekuensi keseluruhan
x¯¯¯=RS+(∑ni=1(fi.ci))∑ni=1fi.p

Cara mencari nilai mean data kelompok.

- Mencari nilai tengah dari data kelompok yang disajikan
- Hasil perkalian dari nilai tengah dengan frekuensi (banyaknya data dari data kelompok)
- Membagi antara hasil perkalian antara nilai tengah dengan frekuensi dengan jumlah frekuensi.

Magang: Feni Listiyani

Contoh soal mean beserta penjelasan lengkap.

1. Hasil ulangan siswa adalah 50, 90, 73, 60, 57, 65, 55, 84, 66, 80. Berapakah rata-rata nilai ulangan siswa tersebut?
Jawab :
Jumlahkan nilai-nilai siswa tersebut, kemudian bagi dengan banyaknya siswa. Banyknya siswa adalah 10 orang.

x¯¯¯=(50+90+73+60+57+65+55+84+66+80):10

x¯¯¯=680:10=68
Jadi, rata-rata data nilai ulangan siswa adalah 68.

2. Rata-rata tinggi badan Ani, Bayu, Cici, Devi, dan Erna adalah 164 cm. Jika tinggi badan Fergusso diikutkan dalam penghitungan rata-rata, maka rata-ratanya menjadi 165 cm. Berapakah tinggi badan Fergusso?
Jawab:

Ada 5 orang dengan rata-rata tinggi badan 164 cm.

Jika ada 6 orang [termasuk Fergusso] maka rata-rata tinggi badannya menjadi 165 cm.

Jumlah tinggi badan 5 orang adalah 5×164=820
Jumlah tinggi badan 6 orang adalah 6×165=990
Selisih jumlah tinggi badan adalah 990−820=170

Jadi, tinggi badan Fergusso adalah 170 cm.

3. Hitung mean dari data berikut ini: 2,3,3,4
Jawab:
x¯¯¯= (2+3+3+4):4
x¯¯¯= 12:4 = 3
Maka mean dari data diatas adalah 3.

4. Nilai matematika 20 siswa kelas XI IPS yaitu 7, 9, 8, 9, 9, 7, 6, 8, 9, 6, 8, 9, 8, 9, 9, 7, 7, 8, 7, 8. Tentukan rata-ratanya.
Jawab:
Urutkan dari yang terkecil hingga terbesarnya
6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9

x¯¯¯= (6+6+7+7+7+7+7+8+8+8+8+8+8+9+9+9+9+9+9+9):20
x¯¯¯= 158 : 20
x¯¯¯= 7,9
Jadi rata-rata dari nilai matematika siswa kelas XI IPS yaitu 7,9 dan yang mendapatkan nilai diatas rata-rata sejumlah 13 siswa.

5. Siswa TKRO mengukur panjang baut yang baru saja dibuatnya. Hasil pengukuran panjang baut tersebut adalah:
3,5 cm sebanyak 4 buah
3,6 cm sebanyak 5 buah
3,7 cm sebanyak 3 buah
3,8 cm sebanyak 2 buah
3,9 cm sebanyak 1 buah
Berapakah mean hasil pengukuran panjang baut di atas?
Jawab:

Untuk menghitung mean data di atas, jumlahkan hasil kali panjang baut dengan banyak baut, kemudian hasilnya dibagi banyaknya baut.

x¯¯¯=(3,5.4+3,6.5+3,7.3+3,8.2+3,9.1):4+5+3+2+1

x¯¯¯=(14+18+11,1+7,6+3,9):15

x¯¯¯=54,6 :15 = 3,64

Jadi, mean hasil pengukuran panjang baut adalah 3,64 cm

6. Hitunglah mean dari data berikut: 13, 18, 13, 14, 13, 16, 14, 21, 13
Jawab:
Nilai mean dapat dihitung dengan menjumlahkan semua data kemudian membaginya dengan banyaknya data:

(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13):9 = 15

Jadi, mean dari data diatas adalah 15.

7. Hitunglah mean dari data berikut: 56, 35, 45, 67, 12, 24, 48, 55, 58, 30
Jawab:
Nilai mean dapat dihitung dengan menjumlahkan semua data kemudian membaginya dengan banyaknya data:

x¯¯¯=(56 + 35 + 45 + 67 + 12 + 24 + 48 + 55 + 58 + 30) ÷ 10 = 43

Jadi, mean dari data diatas adalah 43.

Contoh soal mean beserta penjelasan mudah dipahami.

8. Skor rata-rata dari kelompok yang terdiri dari 20 siswa adalah 65. Dua siswa lainnya yang nilainya 89 dan 85 ditambahkan ke dalam kelompok. Berapa mean atau rata-rata nilai baru dari kelompok siswa tersebut?
Jawab:
Maka, keterangan dan jawabannya dapat ditulis ulang sebagai berikut:

Total nilai = Rata-rata × Jumlah siswa
Total nilai kelompok awal = 65 × 20 = 1.300
Total nilai kelompok baru

= Nilai total kelompok asli + nilai dari 2 siswa baru

= 1.300 + 89 + 85 = 1.474

Jumlah siswa dalam kelompok baru

= Jumlah siswa dalam kelompok awal + Jumlah data baru

= 20 + 2 = 22

Nilai rata-rata kelompok baru = 1.474:22 = 67

9. 10 siswa dalam satu kelas memiliki nilai rata-rata 70. 15 siswa yang tersisa di kelas memiliki nilai rata-rata 80. Berapakah nilai rata-rata dari seluruh kelas?
Jawab:
Nilai total 10 siswa pertama = 10 × 70 = 700

Total nilai sisa 15 siswa = 15 × 80 = 1200

Nilai rata-rata seluruh kelas = (700+1200):25 = 76

10. Hasil ulangan mata pelajaran Matematika yang didapat dari salah seorang murid selama 1 semester adalah:
7.5, 8, 7, 6.5, 7, 7, 6.5, 8, 7.5, 8, 7, 7. Berapakah nilai mean dari data tunggal di atas?
Jawab:
x¯¯¯= (7.5 + 8 + 7 + 6.5 + 7 + 7 + 6.5 + 8 + 7.5 + 8 + 7 + 7) : 12
x¯¯¯= 87 : 12
x¯¯¯= 7,25

Jadi, nilai mean dari murid tersebut adalah 7,25.

11. Data umur mahasiswa International Business School (Bali ) kelas 12.3A.29. Tentukan rata-rata hitung dari data dibawah ini?
21,19,19,20,19,18,18,24,22,25,26,20,21,20,20,19,22,20,25,20
Jawab:
x¯¯¯= (21+19+19+20+19+18+18+24+22+25+26+20+21+20+20+19+22+20+25+20): 20
x¯¯¯= 20,9

12. Hasil pengukuran tinggi badan siswa adalah 163, 165, 161, 170, 164, 155. Berapakah rata-rata tinggi badan siswa?
Jawab:
x¯¯¯= (163+165+161+170+164+155):6
x¯¯¯= 978 : 6
x¯¯¯= 163

13. Sebuah data tunggal disimulasikan dengan urutan sebagai berikut:
2, 2, 3, 4, 5, 5, 6, 7, 7, 8
Pada data tunggal ini, tentukan rata-rata hitung (mean)!
Jawab:
x¯¯¯= (2+2+3+4+5+5+6+7+7+8): 10
x¯¯¯= 49:10
x¯¯¯= 4,9

14. Hasil ulangan siswa adalah 50, 90, 73, 60, 57, 65, 55, 84, 66, 80. Berapakah rata-rata nilai ulangan siswa tersebut?

Jawab:

Jumlahkan nilai-nilai siswa tersebut, kemudian bagi dengan banyaknya siswa. Banyknya siswa adalah 10 orang.

x¯¯¯=(50+90+73+60+57+65+55+84+66+80):10

x¯¯¯=680:10=68
Jadi, rata-rata data nilai ulangan siswa adalah 68.

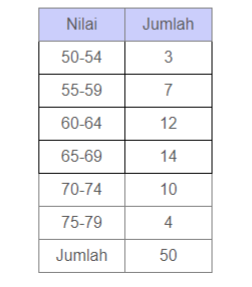
15. Hitunglah mean nilai siswa berikut.

foto: sociomath.my.id

Jawab:
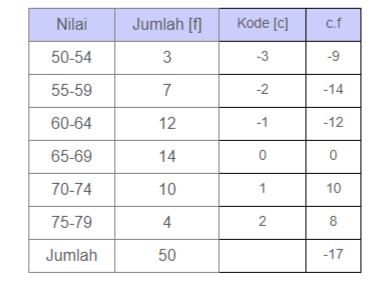
Rata-rata sementara diambil dari titik tengah kelas yang frekuensinya tertinggi, yaitu 65-69, titik tengahnya 67. Sehingga RS=67. Panjang kelas p=5.