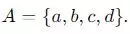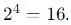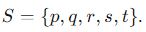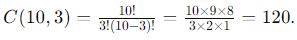15 Contoh soal permutasi disertai penjelasan, persiapan SNBT 2024

Brilio.net - Berlatih soal matematika secara konsisten merupakan langkah penting dalam persiapan untuk Seleksi Nasional Berbasis Tes (SNBT). Berlatih soal matematika membantu meningkatkan pemahaman dan penguasaan konsep-konsep matematika yang diperlukan dalam ujian SNBT.

Dengan mengulang berbagai jenis soal, calon peserta ujian dapat memperdalam pemahaman mereka tentang konsep-konsep matematika yang mendasar, memperluas pengetahuan mereka tentang berbagai macam teknik dan strategi penyelesaian soal, serta meningkatkan kecepatan dan ketepatan dalam menyelesaikan soal.

Salah satu materi matematika dalam tes mencakup soal permutasi. Memahami berbagai tingkat kesulitan soal permutasi yang dapat muncul dalam UTBK, calon peserta ujian dapat mempersiapkan diri mereka dengan lebih baik.

Mereka dapat fokus pada pemahaman konsep-konsep dasar, latihan soal-soal yang menengah, dan juga menantang diri mereka sendiri dengan mencoba menyelesaikan soal-soal permutasi yang lebih rumit. Semakin banyak latihan yang dilakukan dengan berbagai tingkat kesulitan, semakin siap pula calon peserta ujian menghadapi soal-soal permutasi dalam UTBK.

Berikut brilio.net merangkum contoh soal permutasi disertai dengan penjelasan untuk memabantumu dalam persiapan SNBT tahun 2024.

15 Contoh soal pilihan ganda tentang permutasi beserta pembahasannya:

foto: pixabay.com

Soal 1:

Berapa banyak cara menyusun huruf-huruf dalam kata "MATEMATIKA" sehingga huruf vokal tidak berurutan?

A. 720
B. 5040
C. 2880
D. 360
E. 1440

Pembahasan Soal 1:

Huruf-huruf dalam kata "MATEMATIKA" adalah 4 huruf konsonan (M, T, M, K) dan 6 huruf vokal (A, E, A, I, A). Jumlah huruf keseluruhan adalah 10. Kita ingin menghitung berapa banyak cara yang huruf vokalnya tidak berurutan. Kita bisa menghitungnya dengan mempermutasikan 4 huruf konsonan terlebih dahulu, kemudian menempatkan 6 huruf vokal di antara mereka. Jumlah cara adalah

foto: istimewa

karena kita memiliki 4 konsonan dan 7 posisi di antara konsonan-konsonan tersebut.

foto: istimewa

Jumlah totalnya adalah 24 X 7 = 168, jadi jawaban yang tepat adalah D.

Soal 2:

foto: istimewa

Berapa banyak anagram yang mungkin dihasilkan dari himpunan tersebut?

A. 60
B. 120
C. 20
D. 24
E. 10

Pembahasan Soal 2:
Anagram adalah susunan kata atau kalimat yang dibuat dari huruf-huruf suatu kata atau kalimat dengan urutan yang berbeda. Dalam hal ini, kita ingin menghitung berapa banyak cara mengatur angka-angka dalam himpunan S. Karena ada 5 angka dalam himpunan tersebut, maka ada 5! cara. Jadi, jawaban yang tepat adalah D.

Soal 3:
Berapa banyak anagram yang mungkin dihasilkan dari kata "KALKULUS"?

A. 5040
B. 10080
C. 720
D. 2520
E. 40320

Pembahasan Soal 3:
Kata "KALKULUS" memiliki 8 huruf unik. Oleh karena itu, ada 8! cara untuk mengatur huruf-huruf tersebut. Jadi, jawaban yang tepat adalah A.

Soal 4:

foto: istimewa

Berapa banyak himpunan bagian (subset) yang mungkin dihasilkan dari himpunan A?

A. 16
B. 8
C. 4
D. 12
E. 32

Pembahasan Soal 4:
Setiap elemen dalam himpunan bisa atau tidak bisa masuk ke dalam subset. Oleh karena itu, setiap elemen memiliki 2 pilihan, yaitu masuk atau tidak masuk. Karena (A) memiliki 4 elemen, maka jumlah himpunan bagian yang mungkin adalah

foto: istimewa

Jadi, jawaban yang tepat adalah A.

Soal 5:
Berapa banyak kata-kata yang dapat dibuat dari huruf-huruf dalam kata "BOLA", jika tidak ada huruf yang berulang dalam satu kata?

A. 24
B. 120
C. 60
D. 20
E. 10

Pembahasan Soal 5:
Kata "BOLA" memiliki 4 huruf unik. Oleh karena itu, ada 4! cara untuk mengatur huruf-huruf tersebut. Jadi, jawaban yang tepat adalah A.

 

(Magang/Robiul Adil Robani)

 

Soal 6:
Sebuah tim basket terdiri dari 7 pemain. Berapa banyak cara memilih 5 dari 7 pemain tersebut untuk menjadi starting lineup?

A. 21
B. 35
C. 42
D. 70
E. 120

Pembahasan Soal 6:
Kita perlu menghitung kombinasi 5 pemain dari total 7 pemain. Jumlah kombinasi tersebut adalah

foto: istimewa

Jadi, jawaban yang tepat adalah A.

Soal 7:
Berapa banyak bilangan tiga digit yang dapat dibentuk dari angka 1, 2, 3, 4, dan 5 jika angka yang sama boleh muncul lebih dari sekali?

A. 120
B. 125
C. 150
D. 100
E. 1000

Pembahasan Soal 7:
Untuk membentuk bilangan tiga digit, kita memiliki 5 pilihan untuk setiap digit. Oleh karena itu, jumlah totalnya adalah 5 X 5 X 5 = 125. Jadi, jawaban yang tepat adalah B.

Soal 8:

foto 8: istimewa

Berapa banyak permutasi yang mungkin dihasilkan dari himpunan tersebut?

A. 120
B. 60
C. 20
D. 24
E. 5!

foto: pixabay.com

Pembahasan Soal 8:
Dalam permutasi, urutan penting. Jumlah permutasi dari himpunan S yang terdiri dari 5 elemen adalah 5! atau 120. Jadi, jawaban yang tepat adalah A.

Soal 9:
Berapa banyak cara yang berbeda untuk mengatur 5 buku di rak buku?

A. 20
B. 60
C. 120
D. 720

Pembahasan Soal 9
Untuk mengatur 5 buku di rak buku, kita menggunakan konsep permutasi. Jumlah cara pengaturan adalah 5! karena ada 5 buku yang diatur, dan urutannya penting. Oleh karena itu, jawaban yang tepat adalah C.

 

Soal 10:
Seorang pemilik toko buku memiliki 6 buku matematika, 4 buku fisika, dan 3 buku kimia. Jika ia ingin menampilkan 3 buku secara berdampingan di jendela toko, berapa banyak cara yang berbeda ia bisa memilih buku-buku tersebut?

A. 288
B. 120
C. 60
D. 750

Pembahasan Soal 10
Jumlah buku matematika, fisika, dan kimia yang dimiliki oleh pemilik toko adalah masing-masing 6, 4, dan 3. Karena ia ingin menampilkan 3 buku secara berdampingan, maka kita harus menghitung permutasi untuk masing-masing jenis buku, kemudian menjumlahkannya. Jumlahnya adalah P(6,3) + P(4,3) + P(3,3). Setelah dihitung, kita mendapatkan 6! + 4! + 3! = 720 + 24 + 6 = 750. Oleh karena itu, jawaban yang tepat adalah D

Soal 11:
Berapa banyak cara yang berbeda untuk mengatur huruf-huruf dalam kata "KALKULUS"?

A. 5040
B. 720
C. 2520
D. 840

Pembahasan Soal 11:
Kata "KALKULUS" memiliki 8 huruf unik. Jumlah cara pengaturannya adalah 8! karena setiap huruf dianggap unik dan urutannya penting. Oleh karena itu, jawaban yang tepat adalah A.

Soal 12:

foto: istimewa

Berapa banyak permutasi yang mungkin dihasilkan dari himpunan tersebut?

A. 12
B. 24
C. 48
D. 4

Pembahasan Soal 12:
Dalam permutasi, urutan penting. Jumlah permutasi dari himpunan S yang terdiri dari 4 elemen adalah 4! atau 24. Oleh karena itu, jawaban yang tepat adalah B.

Soal 13:
Sebuah band terdiri dari 5 anggota. Berapa banyak cara yang berbeda untuk mengatur posisi mereka dalam barisan?

A. 20
B. 120
C. 240
D. 720

Pembahasan Soal 13:
Untuk mengatur posisi 5 anggota band dalam barisan, kita menggunakan konsep permutasi. Jumlah cara pengaturan adalah 5! karena ada 5 anggota dan urutannya penting. Oleh karena itu, jawaban yang tepat adalah D.

Soal 14:
Berapa banyak anagram yang mungkin dihasilkan dari kata "MATHEMATICS"?

A. 3628800
B. 1440
C. 720
D. 40320

Pembahasan Soal 14:
Kata "MATHEMATICS" memiliki 11 huruf unik. Jumlah anagram yang bisa dibuat dari kata tersebut adalah 11! karena setiap huruf dianggap unik dan urutannya penting. Oleh karena itu, jawaban yang tepat adalah A.

Soal 15:
Seorang guru ingin memilih 3 siswa dari kelasnya untuk mengikuti lomba matematika. Jika kelasnya terdiri dari 10 siswa, berapa banyak cara guru tersebut bisa memilih 3 siswa?

A. 30
B. 90
C. 120
D. 720

Pembahasan Soal 15:
Kita harus menghitung kombinasi 3 siswa dari total 10 siswa. Jumlah kombinasi tersebut adalah

foto: istimewa

Oleh karena itu, jawaban yang tepat adalah C.