Brilio.net - Mata pelajaran Matematika memang kadang membuat orang pusing dalam mengerjakannya. Begitu banyak materi dan rumus membuat kamu pastinya males untuk belajar. Tapi kali ini buat kamu yang mau belajar dan mendalami materi Matematika, coba kamu perhatikan dan praktik pada soal-soal yang disediakan oleh gurumu.
Salah satu materi Matematika yang wajib kamu kuasai adalah SPLDV. Kamu pernah mendengar apa itu SPLDV? Untuk lebih detail kamu wajib simak penjelasan di bawah ini. Berikut brilio.net rangkum dari berbagai sumber pada Rabu (26/10).
Pengertian SPLDV.
SPLDV atau kepanjangan dari Sistem Persamaan Linear Dua Variable merupakan suatu sistem dari persamaan maupun bentuk dari relasi yang sama dengan bentuk aljabar yang mempunyai dua variabel dan juga berpangkat satu, apabila digambarkan dalam suatu grafik maka akan membentuk garis yang lurus.
Ciri-ciri SPLDV (Sistem Persamaan Linear Dua Variable).
- Menggunakan relasi atau tanda sama dengan (=)
- Mempunyai dua variabel
- Kedua variabel mempunyai derajat satu atau berpangkat satu
Hal-hal yang berhubungan dengan SPLDV.
1. Suku
Suku merupakan bentuk aljabar yang terdiri dari variabel, koefisien, dan konstanta, dan setiap suku dipisahkan dengan tanda baca penjumlahan maupun pengurangan.
Contoh: 7x - y + 3, jadi suku-suku dari persamaan tersebut yaitu 7x, -y, dan 3.
2. Variabel
Variabel merupakan suatu perubahan ataupun pengganti sebuah bilangan dan dilambangkan dengan huruf seperti x dan y.
Contoh: Sasa mempunyai 5 boneka ikan dan 2 boneka beruang, apabila dituliskan dalam bentuk persamaan yaitu:
- Boneka ikan = X
- Boneka beruang = Y
- Persamaannya: 5x + 2y.
3. Koefisien.
Koefisien merupakan suatu bilangan yang menyatakan banyaknya suatu jumlah variabel yang satu jenis.
Contoh: Sani mempunyai 3 baju dan 4 celana, apabila dituliskan dalam bentuk persamaan yaitu:
- Baju = X dan celana = Y
- Persamaannya: 3x + 4y
- 2 dan 5 merupakan koefisien, 2 yaitu koefisiennya X dan 5 koefisiennya Y.
4. Konstanta.
Konstanta merupakan suatu bilangan yang tidak diikuti oleh variabel, maka nilainya tetap maupun konstan untuk berapapun nilai perubahannya.
Contoh: 4x + 8y + 16, dari persamaan tersebut konstanta yaitu 16, karena nilainya 16 maka tetap dan tidak terpengaruh dengan berapapun variabelnya.
1-5 Contoh soal SPLDV (Sistem Persamaan Linear Dua Variable) lengkap dengan ulasan.
1. Tentukan himpunan dari penyelesaian dan dari persamaan berikut ini yaitu x + 3y = 15 dan 3x + 6y = 30 ?
Penyelesaiannya :
Diketahui :
Persamaan Pertama = x + 3y = 15
Persamaan yang Kedua = 3x + 6y = 30
Langkah yang Pertama : Ubahlah dari salah satu persamaan dan carilah yang termudah.
X + 3y = 15 > X = -3y + 15
Langkah yang Kedua : Subsititusi nilai X = -3y + 15 ke dalam persamaan yang kedua untuk mencari nilai Y, maka hasilnya sebagai berikut yaitu :
3x + 6y = 30
3 (-3y +15) + 6y = 30
-9y + 45 + 6y = 30
-3y = 30 45
-3y = -15
y = 5
Langkah yang Ketiga : Selanjutnya carilah nilai x maka, gunakanlah salah satu dari persamaan boleh itu dari persamaan yang pertama maupun yang kedua :
Dari Persamaan yang Pertama :
+ 3y = 15
X + 3 (5) = 15
X + 15 = 15
X = 0
Persamaan yang Kedua :
3x + 6y = 30
3x + 6 (5) = 30
3x + 30 = 30
3x = 0
X = 0
Langkah yang Keempat : Maka nilai himpunannya jadi, = { 0 , 5 }
2. Tentukan penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , apabila x = a dan y = b . Maka tentukanlah nilai a dan b nya !
Penyelesaiannya :
Diketahui :
Persamaan 1 = 3x+ 5y = 16
Dan Persamaan 2 = 4x + y = 10
Langkah yang Pertama yaitu tentukanlah variabelnya yang mana akan di eliminasi terlebih dahulu perhatikan penyelesaian di bawah ini :
3x+ 5y = 16 | x1 | <=> 3x + 5y = 16 . . . . (1)
4x + y = 10 | x5 | <=> 20x + 5y = 50 . . . (2)
Dari persamaan (1) dan juga (2), dapat kita eliminasikan dan dapat menghasilkan yaitu :
20x + 5y = 50
3x + 5y = 16 _
17 x + 0 = 34
x = 34 / 17
x = 2
Langkah yang Kedua selanjutnya, marilah kita lakukan langkah yang sama namun kali ini harus sama dengan x nya , maka caranya yaitu sebagai berikut :
3x+ 5y = 16 | x4 | <= > 12 x + 20y = 64 . . .(3)
4x + y = 10 | x3 | <=> 12x + 3y = 30 . . . .(4)
Langkah yang Ketiga Persamaan (3) dan juga (4) , marilah kita eliminasikan untuk menghasilkan nilai y nya :
12 x + 20y = 64
12x + 3y = 30 _
0 + 17y = 34
y = 2
Jadi , Himpunannya = { 2 ,2 } , dan pada nilai a dan b yaitu : a= x = 2 dan b = y = 2
3. Maka diketahui pada persamaan x + 3y = 15 dan 3x + 6y = 30, ini maka harus menggunakan dengan cara metode campuran dan tentukanlah himpunan penyelesaiannya !
Penyelesaiannya :
Diketahui :
Persamaan 1 = x + 3y = 15
Persamaan 2 = 3x + 6y = 30
Langkah yang Pertama kita harus menggunakan metode eliminasi :
x + 3y = 15 | x3| <=> 3x +9x = 45
3x + 6y = 30 | x1| <=> 3x + 6y = 30 _
0 + 3y = 15
Y = 5
Langkah yang Kedua kita juga harus menggunakan dengan cara Metode Substusi :
X + 3y = 15
X + 3.5 = 15
X + 15 = 15
X = 0
Jadi, himpunan dari penyelesaian soal di atas tadi yaitu Himpunan ={ 0 , 5 }.
4. Titik potong untuk Persamaan yang ke 2 yaitu x y = 1
Cara menentukan titik potong pada sumbu -x maka syaratnya y = 0
X y = 1
X 0 = 1
X = 1
Maka titik potong nya yaitu (1,0).
Cara menentukan titik potong pada sumbu -y maka syaratnya x = 0
X y = 1
0 y = 1
Y = -1
Maka titik potong nya yaitu (0,-1).
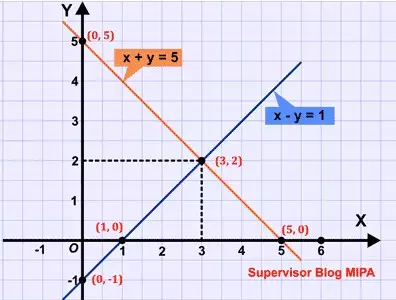
Pada langkah yang kedua, Gambarkanlah grafik dari masing masing titik potong dari kedua persamaan di atas tadi, maka hasilnya bisa dilihat dari gambar di bawah ini yaitu :
foto: edmodo.id
SPLDV metode grafik.
Apabila kita lihat dari gambar grafik di atas, maka titik potong dari ke 2 grafik tersebut ialah di titik (3, 2).
Maka hasil dari himpunan penyelesaiannya ialah {3,2}.
5. Ibu Ervin berbelanja di pasar, ia membeli 5 kg bakso sapi dan 4 kg bakso ikan dengan harga Rp. 550.000. Di pasar yang sama, Bu Feni membeli 4 kg bakso sapi dan 5 kg bakso ikan dengan harga Rp. 530.000. Sedangkan ibu ijah membeli 2 kg bakso spi dan 3 kg bakso ikan. Bu Ijah harus membayar sebesar...
Jawab:
x = harga bakso sapi
y = harga bakso ikan
Diperoleh SPLDV sebagai berikut:
5x+4y = 550.000 x 4 = 20x + 16y = 2.200.000
4x + 5y = 530.000 x 5 = 20x + 25y = 2.650.000
y = 50.000
Substitusikan y = 50.000 ke persamaan:
5x + 4y = 550.000
5x + 4(50.000) = 550.000
5x = 550.000 - 200.000
x = 70.000
Lalu cari harga yang harus dibayar bu Ijah
2x + 3y = 2(70.000) + 3(50.000) = 140.000 + 150.000 = 290.000
Jadi ibu ijah harus membayar sebesar Rp. 290.000
Magang: Feni Listiyani