20 Contoh soal belah ketupat, lengkap dengan rumus luas dan keliling beserta penjelasannya

Brilio.net - Belah ketupat merupakan salah satu bangun datar segiempat dengan karakteristik unik. Bentuknya menyerupai ketupat atau diamond, membuatnya mudah dikenali dalam berbagai konteks. Belah ketupat termasuk dalam kategori jajar genjang sama kaki, namun memiliki keistimewaan berupa empat sisi yang sama panjang.

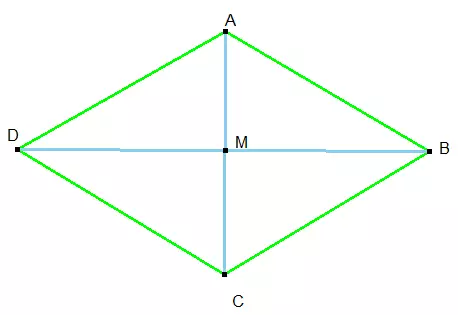
Keunikan belah ketupat terletak pada sifat-sifatnya yang simetris dan teratur. Diagonalnya saling berpotongan tegak lurus, membagi dua sama besar sudut-sudut di setiap titik sudutnya. Karakteristik ini menjadikan belah ketupat sebagai objek menarik dalam pembelajaran geometri.

Pemahaman mendalam tentang belah ketupat sangat bermanfaat dalam berbagai aplikasi praktis. Pengetahuan ini dapat diterapkan dalam arsitektur, desain, dan berbagai bidang lain yang memerlukan perhitungan luas atau keliling bangun datar.

Berikut brilio.net himpun ciri-ciri, rumus, dan contoh soal belah ketupat dari berbagai sumber pada Kamis (15/8).

Ciri-ciri belah ketupat

contoh soal belah ketupat
Unsplash.com

Belah ketupat memiliki beberapa ciri khas yang membedakannya dari bangun datar lain:

1. Memiliki empat sisi sama panjang
2. Sisi-sisi yang berhadapan sejajar
3. Sudut-sudut yang berhadapan sama besar
4. Diagonal-diagonalnya saling berpotongan tegak lurus
5. Diagonal-diagonal membagi dua sama besar sudut-sudut belah ketupat
6. Diagonal-diagonal merupakan sumbu simetri
7. Memiliki dua tingkat simetri putar
8. Dapat dibentuk dari dua segitiga sama kaki yang kongruen
9. Semua diagonalnya membentuk segitiga-segitiga yang kongruen
10. Dapat menempati bingkainya dengan empat cara berbeda

Rumus belah ketupat

contoh soal belah ketupat
Wikipedia.com

Pemahaman rumus belah ketupat penting untuk menyelesaikan berbagai persoalan terkait bangun datar ini. Terdapat dua rumus utama yang perlu diketahui: rumus luas dan rumus keliling belah ketupat.

Rumus luas belah ketupat digunakan untuk menghitung area yang dibatasi oleh keempat sisi belah ketupat. Luas belah ketupat dapat dihitung dengan menggunakan rumus:

Luas = 1/2 d1 d2

Keterangan:
d1 = panjang diagonal pertama
d2 = panjang diagonal kedua

Rumus ini menunjukkan bahwa luas belah ketupat merupakan setengah dari hasil perkalian kedua diagonalnya.

Sementara itu, rumus keliling belah ketupat digunakan untuk menghitung panjang total semua sisi belah ketupat. Keliling belah ketupat dapat dihitung dengan rumus:

Keliling = 4 s

Keterangan:
s = panjang sisi belah ketupat

Rumus ini menunjukkan bahwa keliling belah ketupat sama dengan empat kali panjang sisinya, mengingat semua sisi belah ketupat memiliki panjang yang sama.

Contoh soal belah ketupat

contoh soal belah ketupat
Pixabay.com

Berikut ini disajikan 20 contoh soal belah ketupat beserta pembahasannya, meliputi perhitungan luas dan keliling.

Contoh Luas Belah Ketupat:

1. Sebuah belah ketupat memiliki diagonal 8 cm dan 12 cm. Hitunglah luasnya.
Pembahasan:
Luas = 1/2 d1 d2
Luas = 1/2 8 12 = 48 cm

2. Diagonal-diagonal sebuah belah ketupat berukuran 10 cm dan 15 cm. Berapakah luasnya?
Pembahasan:
Luas = 1/2 10 15 = 75 cm

3. Luas sebuah belah ketupat adalah 60 cm. Jika salah satu diagonalnya 10 cm, berapakah panjang diagonal lainnya?
Pembahasan:
60 = 1/2 10 d2
d2 = 60 2 10 = 12 cm

4. Sebuah belah ketupat memiliki luas 120 cm dan salah satu diagonalnya 16 cm. Hitunglah panjang diagonal lainnya.
Pembahasan:
120 = 1/2 16 d2
d2 = 120 2 16 = 15 cm

5. Diagonal-diagonal belah ketupat berukuran 18 cm dan 24 cm. Berapakah luasnya?
Pembahasan:
Luas = 1/2 18 24 = 216 cm

6. Luas sebuah belah ketupat adalah 150 cm. Jika panjang salah satu diagonalnya 25 cm, berapakah panjang diagonal lainnya?
Pembahasan:
150 = 1/2 25 d2
d2 = 150 2 25 = 12 cm

7. Sebuah belah ketupat memiliki diagonal 14 cm dan 20 cm. Hitunglah luasnya.
Pembahasan:
Luas = 1/2 14 20 = 140 cm

8. Luas belah ketupat adalah 96 cm. Jika perbandingan panjang diagonalnya 3:4, berapakah panjang masing-masing diagonal?
Pembahasan:
Misalkan d1 = 3x dan d2 = 4x
96 = 1/2 3x 4x
96 = 6x
x = 16
x = 4
d1 = 3 4 = 12 cm
d2 = 4 4 = 16 cm

9. Sebuah belah ketupat memiliki luas 180 cm. Jika panjang salah satu diagonalnya 18 cm, berapakah panjang diagonal lainnya?
Pembahasan:
180 = 1/2 18 d2
d2 = 180 2 18 = 20 cm

10. Diagonal-diagonal belah ketupat berukuran 30 cm dan 40 cm. Hitunglah luasnya.
Pembahasan:
Luas = 1/2 30 40 = 600 cm

Contoh Keliling Belah Ketupat:

11. Sebuah belah ketupat memiliki panjang sisi 9 cm. Berapakah kelilingnya?
Pembahasan:
Keliling = 4 s = 4 9 = 36 cm

12. Keliling sebuah belah ketupat adalah 48 cm. Berapakah panjang sisinya?
Pembahasan:
48 = 4 s
s = 48 4 = 12 cm

13. Sebuah belah ketupat memiliki panjang diagonal 16 cm dan 12 cm. Jika kelilingnya 40 cm, berapakah panjang sisinya?
Pembahasan:
Keliling = 4 s
40 = 4 s
s = 40 4 = 10 cm

14. Panjang sisi sebuah belah ketupat adalah 15 cm. Hitunglah kelilingnya.
Pembahasan:
Keliling = 4 15 = 60 cm

15. Sebuah belah ketupat memiliki keliling 72 cm. Berapakah panjang sisinya?
Pembahasan:
72 = 4 s
s = 72 4 = 18 cm

16. Keliling sebuah belah ketupat adalah 56 cm. Hitunglah panjang sisinya.
Pembahasan:
56 = 4 s
s = 56 4 = 14 cm

17. Sebuah belah ketupat memiliki panjang sisi 11 cm. Berapakah kelilingnya?
Pembahasan:
Keliling = 4 11 = 44 cm

18. Keliling sebuah belah ketupat adalah 84 cm. Berapakah panjang sisinya?
Pembahasan:
84 = 4 s
s = 84 4 = 21 cm

19. Sebuah belah ketupat memiliki panjang diagonal 24 cm dan 18 cm. Jika kelilingnya 68 cm, berapakah panjang sisinya?
Pembahasan:
68 = 4 s
s = 68 4 = 17 cm

20. Panjang sisi sebuah belah ketupat adalah 13 cm. Hitunglah kelilingnya.
Pembahasan:
Keliling = 4 13 = 52 cm

Contoh soal belah ketupat ini memberikan gambaran mengenai variasi persoalan yang dapat dihadapi terkait bangun datar belah ketupat. Pemahaman mendalam tentang rumus luas dan keliling belah ketupat sangat penting untuk menyelesaikan soal-soal tersebut dengan tepat. Latihan mengerjakan berbagai tipe soal akan meningkatkan kemampuan dalam menerapkan konsep belah ketupat pada situasi yang berbeda-beda.