Cara menghitung rumus luas permukaan bola dan contoh soalnya

Brilio.net - Sejak kecil kita telah diperkenalkan dengan berbagai bentuk benda-benda sekitar kita. Misalnya bentuk kotak, segitiga, persegi panjang, atau benda dengan bentuk bulat.

Nah, dalam perhitungan ilmu matematika, benda dengan bentuk bulat umumnya dikenal dengan sebutan bola. Permukaan bola adalah himpunan titik-titik yang berjarak sama dari satu titik pusat dalam ruang tiga dimensi. Permukaan bola juga disebut sebagai kulit bola atau selimut bola.

Bisa dikatakan permukaan bola merupakan objek geometri dua dimensi yang membentuk batas dari bola, yaitu bangun ruang tiga dimensi yang terdiri dari titik-titik yang berjarak kurang dari atau sama dengan jari-jari dari titik pusatnya.

Untuk menghitung rumus luas permukaan bola nggak terlalu sulit kok. Kamu hanya perlu memahami konsep rumusnya maka akan lebih mudah menjawab soal-soal tentang luas permukaan bola ini.

Berikut cara menghitung rumus luas permukaan bola dan contoh soalnya, yang dilansir brilio.net dari berbagai sumber, Senin (4/9).

Pengertian rumus luas permukaan bola.

foto: Istimewa

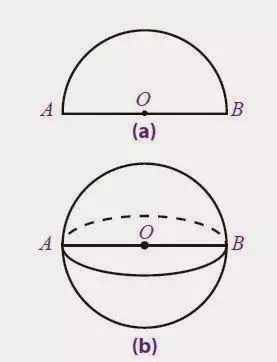
Dapat diamati bahwa pada gambar (a) menunjukkan bentuk setengah lingkaran yang apabila diputar hinggga satu putaran penuh atau mencapai 360 derajat, dari titik A ke B, B ke A maka memperoleh sebuah bangun bulat yang terdapat pada gambar (b). Bulatan tersebut dikenal dengan permukaan bola.

Permukaan bola adalah bagian luar dari objek tiga dimensi yang disebut bola atau sphere. Permukaan bola adalah bidang datar atau kurva yang mengelilingi bola dan terdiri dari semua titik di sekitar bola yang memiliki jarak yang sama dari titik pusatnya. Dengan kata lain, permukaan bola adalah "lapisan" atau "kulit" bola yang menyusun batas atau tepinya.

Ciri-ciri permukaan bola adalah sebagai berikut:

1. Semua Titik Sama Jauh:

Dari pusat bola ke setiap titik di permukaannya, jaraknya sama. Ini berarti setiap titik di permukaan bola memiliki jarak yang sama dengan radius bola.

2. Bidang Tak Berbatas

Permukaan bola adalah bidang yang tak berbatas dan bersifat kontinu. Kamu tidak dapat menunjukkan titik akhir pada permukaan bola karena setiap titik pada bola memiliki titik yang sejajar dengannya pada permukaan tersebut.

3. Bidang Dua Dimensi

Meskipun bola adalah objek tiga dimensi, permukaan bola adalah bidang datar dua dimensi yang membungkus bola.

Dalam matematika, luas permukaan bola dapat dihitung menggunakan rumus berikut:

Luas Permukaan Bola = 4πr²

Di mana:
- "Luas Permukaan Bola" adalah luas total dari permukaan bola.

- "π" adalah pi (sekitar 3,14159).

- "r" adalah radius bola, yaitu jarak dari pusat bola ke titik mana pun pada permukaannya.

Cara menghitung rumus luas permukaan bola.

foto: Istimewa

Rumus untuk menghitung luas permukaan bola adalah sebagai berikut:

Luas Permukaan Bola = 4πr^2

Di sini:

- "Luas Permukaan Bola" adalah luas total dari permukaan bola.

- "π" adalah pi (sekitar 3,14159).

- "r" adalah radius bola, yaitu jarak dari pusat bola ke titik mana pun pada permukaannya.

Untuk menghitung luas permukaan bola, langkah-langkahnya adalah sebagai berikut:

1. Tentukan nilai radius (r) bola. Ini adalah jarak dari pusat bola ke titik mana pun pada permukaannya.

2. Gunakan rumus di atas: Luas Permukaan Bola = 4πr²

3. Gantilah nilai "r" dalam rumus dengan nilai radius yang telah ditentukan.

4. Hitung hasilnya.

Contoh:
Misalkan si Budi memiliki bola dengan radius 5 cm. Untuk menghitung luas permukaan bola tersebut:

Luas Permukaan Bola = 4π(5 cm)²

Luas Permukaan Bola = 4π(25 cm²)

Luas Permukaan Bola = 100π cm²

Jadi, luas permukaan bola dengan radius 5 cm adalah 100π cm² atau sekitar 314,16 cm².

Contoh soal luas permukaan bola dan pembahasannya.

foto: Istimewa

1. Sebuah bola memiliki jari-jari 5 cm. Berapakah luas permukaan bola tersebut?

Jawaban:

Luas permukaan bola = 4 x π x r²

Luas permukaan bola = 4 x 3,14 x 5²

Luas permukaan bola = 4 x 3,14 x 25

Luas permukaan bola = 314 cm²

2. Sebuah balon berbentuk bola memiliki diameter 20 cm. Berapakah luas permukaan balon tersebut?

Jawaban:

Diameter bola = 2 x jari-jari bola

Jari-jari bola = diameter bola / 2

Jari-jari bola = 20 / 2

Jari-jari bola = 10 cm

Luas permukaan bola = 4 x π x r²

Luas permukaan bola = 4 x 3,14 x 10²

Luas permukaan bola = 4 x 3,14 x 100

Luas permukaan bola = 1256 cm²

3. Sebuah globe berbentuk bola memiliki luas permukaan yang sama dengan luas lingkaran yang memiliki jari-jari 21 cm. Berapakah jari-jari globe tersebut?

Jawaban:

Luas permukaan bola = luas lingkaran

4 x π x r² = π x R²

di mana r adalah jari-jari globe dan R adalah jari-jari lingkaran.

4 x r = R²

r²= R² / 4

r = akar kuadrat dari (R² / 4)

r = akar kuadrat dari ((21)² / 4)

r = akar kuadrat dari (441 / 4)

r = akar kuadrat dari (110,25)

r = sekitar 10,5 cm

4. Sebuah bangun ruang berbentuk setengah bola memiliki luas permukaan seluruhnya sebesar 462 cm². Berapakah jari-jari bangun ruang tersebut?