Macam-macam rumus sin cos tan, lengkap dengan contoh soal dan pembahasan yang mudah dipahami

Brilio.net - Dalam matematika ada cabang ilmu yang membahas tentang hubungan sisi serta sudut yang ada pada segitiga. Materi ini biasa disebut dengan trigonometri. Materi ini biasanya akan mulai kamu temui saat memasuki kelas 10 pada jenjang SMA.

Hubungan sudut tersebut umumnya disebut sebagai perbandingan sinus, kosinus, dan juga tangen. Kalau disingkat maka menjadi sin cos tan. Kamu tentu masih ingat bukan, kalau segitiga siku-siku punya tiga sisi yaitu depan, samping, dan miring? Lalu, jumlah dari ketiga sudut itu hasilnya 180.

Nah, materi dasar tersebut yang akan kamu pakai untuk mempelajari sin cos tan. Dalam menghitung sudutnya, tentu sudah ada rumus-rumus sin cos tan yang bisa kamu gunakan. Supaya nggak bingung, langsung saja yuk pelajari macam-macam rumus sin cos tan, lengkap dengan contoh soal dan pembahasan yang mudah dipahami, dihimpun brilio.net dari berbagai sumber, Jumat (22/9).

Pengertian sin cos tan

foto: freepik.com

Sin, cos, dan tan adalah tiga fungsi trigonometri yang mendasar dan sangat penting dalam matematika. Mereka digunakan untuk menghubungkan sudut dalam segitiga siku-siku dan memodelkan berbagai fenomena dalam ilmu pengetahuan. Berikut adalah pengertian dari ketiga fungsi trigonometri ini:

1. Sin (Sinus):

Pengertian: Sinus (sin) dari suatu sudut dalam trigonometri adalah rasio panjang sisi berlawanan terhadap sudut tersebut dengan panjang sisi miring dalam segitiga siku-siku.

2. Cos (Kosinus):

Kosinus (cos) dari suatu sudut dalam trigonometri adalah rasio panjang sisi yang berdekatan dengan sudut tersebut dengan panjang sisi miring dalam segitiga siku-siku.

3. Tan (Tangen):

Tangen (tan) dari suatu sudut dalam trigonometri adalah rasio panjang sisi berlawanan dengan sudut tersebut terhadap panjang sisi yang berdekatan dalam segitiga siku-siku.

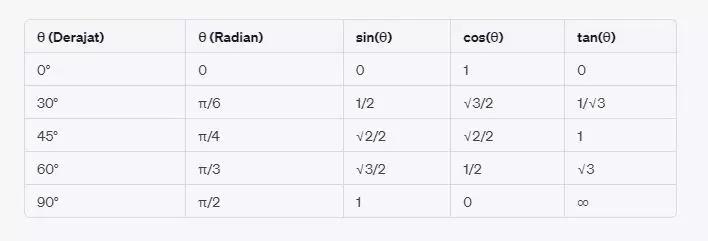
Tabel sin cos tan

foto: Istimewa

Dalam tabel di atas, θ adalah sudut dalam derajat dan radian. Kamu dapat mengganti nilai θ sesuai kebutuhan untuk menghitung nilai sin, cos, dan tan untuk sudut tertentu. Pastikan untuk mengonversi sudut dari derajat ke radian jika diperlukan, dengan mengingat bahwa 180° = π radian. Nilai-nilai trigonometri yang lebih spesifik (seperti sin(37°) atau cos(53°)) dapat dihitung dengan rumus sin, cos, dan tan yang sesuai.

Rumus dasar sin cos tan

1. Rumus sin (sinus)

Sinus dari sudut θ (dalam derajat) dinyatakan sebagai rasio panjang sisi berlawanan terhadap sudut tersebut terhadap panjang sisi miring segitiga siku-siku. Rumus sin adalah:

foto: istimewa

Sin(θ)= Panjang sisi miring/panjang sisi berlawanan

2. Rumus cos (kosinus)

Kosinus dari sudut θ (dalam derajat) dinyatakan sebagai rasio panjang sisi yang berdekatan dengan sudut tersebut terhadap panjang sisi miring segitiga siku-siku. Rumus cos adalah:

foto: istimewa

Cos(θ)= Panjang sisi miring/panjang sisi berdekatan

3. Rumus tan (tangen)

Tangen dari sudut θ (dalam derajat) dinyatakan sebagai rasio panjang sisi berlawanan dengan sudut tersebut terhadap panjang sisi yang berdekatan. Rumus tan adalah:

foto: istimewa

Tan(θ)= Panjang sisi berdekatan/panjang sisi berlawanan

Rumus sin cos tan pada sudut khusus

Beberapa sudut khusus yang memiliki nilai sin, cos, dan tan yang mudah diingat adalah:

sin(0°) = 0, cos(0°) = 1, tan(0°) = 0
sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1
sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3
sin(90°) = 1, cos(90°) = 0 (nilai tan(90°) tidak terdefinisi)

Rumus sin cos tan sudut ganda

a. sin(2θ) = 2sin(θ)cos(θ)

b. cos(2θ) = cos²(θ) - sin²(θ)

c. tan(2θ) = \frac{2tan(θ)}{1 - tan²(θ)}

Contoh-contoh soal tentang sin cos tan

foto: freepik.com

1. Hitung nilai sin(30°) + cos(30°).

Pembahasan:
sin(30°) = 1/2 dan cos(30°) = √3/2. Jadi,
sin(30°) + cos(30°) = 1/2 + √3/2 = (1 + √3)/2.

2. Hitung nilai tan(45°) × cos(45°).

Pembahasan:
tan(45°) = 1 dan cos(45°) = √2/2. Jadi,
tan(45°) × cos(45°) = 1 × (√2/2) = √2/2.

3. Jika sin(θ) = 0, apa nilai dari cos(θ)?

Pembahasan:
Jika sin(θ) = 0, ini berarti θ adalah kelipatan dari 180 derajat (n × 180°), di mana cos(θ) = 1 atau -1 tergantung pada kelipatannya.

4. Hitung nilai tan(60°) - sin(30°).

Pembahasan:
tan(60°) = √3 dan sin(30°) = 1/2. Jadi,
tan(60°) - sin(30°) = √3 - 1/2.

5. Jika cos(α) = 0, apa nilai dari sin(α)?

Pembahasan:
Jika cos(α) = 0, ini berarti α adalah kelipatan ganjil dari 90 derajat (n × 90°), di mana sin(α) = 1 atau -1 tergantung pada kelipatannya.

6. Hitung nilai sin(π/6) + cos(π/3).

Pembahasan:
sin(π/6) = 1/2 dan cos(π/3) = 1/2. Jadi,
sin(π/6) + cos(π/3) = 1/2 + 1/2 = 1.

7. Jika tan(β) = 2, apa nilai dari cos(β)?

Pembahasan:
Jika tan(β) = 2, ini berarti β adalah sudut yang sesuai dengan sin(β) = 2/√5 dan cos(β) = 1/√5.

8. Hitung nilai tan(75°) × cos(15°).

Pembahasan:
tan(75°) = √3 + 1 dan cos(15°) = √6 - √2. Jadi,
tan(75°) × cos(15°) = (√3 + 1) × (√6 - √2).

9. Jika sin(x) = 0,5 dan x berada di kuadran kedua, berapa nilai cos(x)?

Pembahasan:
Kuadran kedua berarti sudut x antara 90° dan 180°. Jadi, cos(x) adalah negatif. Dari sin(x) = 0,5, kita tahu bahwa x = 30° atau x = 150°. Jadi, cos(x) = -√3/2.

10. Hitung nilai tan(α) jika cos(α) = 0 dan α berada di kuadran ketiga.

Pembahasan:
Kuadran ketiga berarti sudut α antara 180° dan 270°. Jadi, sin(α) adalah negatif. Jika cos(α) = 0, maka α adalah kelipatan ganjil dari 90 derajat, sehingga sin(α) = -1. Maka, tan(α) = sin(α) / cos(α) = -1 / 0 = Tidak Terdefinisi.