Brilio.net - Memahami rumus phytagoras memang cukup rumit. Namun, jika ditelusuri lebih jauh ternyata dalam memahami rumus phytagoras matematika tidak begitu rumit. Kamu hanya perlu memahami konsep dasar dari rumus phytagoras ini.
Umumnya konsep dasar teorema phytagoras berbunyi "Di dalam sebuah segitiga siku-siku diberlakukan kuadrat dari sisi miring sama dengan jumlah kuadrat dari sisi-sisi lainnya" Hal ini berarti ketiga sisi segitiga siku-siku mempunyai hubungan yang saling terikat satu sama lain. Keterikatan tersebut membuat segitiga siku-siku memiliki nilai yang sama.
Oleh sebab itu, ketika kamu diminta mencari salah satu sisi segitiga yang tidak diketahui nilainya maka kerap digunakan teorema phytagoras ini. Biar makin memahami tentang rumus phytagoras, berikut brilio.net berikan ulasan lengkap tentang pengertian rumus phytagoras lengkap dengan cara menghitung dan cirinya, dilansir dari berbagai sumber, Selasa (29/8).
Pengertian rumus phytagoras.
foto: pixabay.com
Rumus Pythagoras adalah salah satu prinsip dasar dalam matematika yang berkaitan dengan hubungan antara panjang sisi-sisi segitiga siku-siku. Rumus ini dinamai dari matematikawan Yunani kuno bernama Pythagoras, yang dikenal karena kontribusinya dalam mengembangkan geometri dan teorema ini.
Hal ini berarti, jauh sebelum rumus phytagoras ini kita pelajari dan gunakan saat ini ternyata sudah ada jauh sejak 1900-1600 SM. Kala itu, ada orang Babilonia dan Cina yang baru menyadari suatu fakta bahwa segitiga itu terdiri dari panjang sisi 3, 4, dan 5 satuan panjang akan membentuk segitiga siku siku.
Nggak hanya itu, teorema pythagoras juga disebutkan dalam Baudhayana Sulbasutra India yang ditulis antara 800 dan 400 SM tentang Tripel Pythagoras. Hingga akhirnya teorema tersebut kerap disebut sebagai Pythagoras. Walau begitu, belum dapat dipastikan secara pasti apakah Pythagoras adalah orang pertama yang menemukan hubungan antara sisi segitiga siku siku, karena tidak ada teks yang menuliskan tentangnya.
Rumus Pythagoras dinyatakan dalam bentuk persamaan matematika:
C2 = a2 + b2
foto: Istimewa
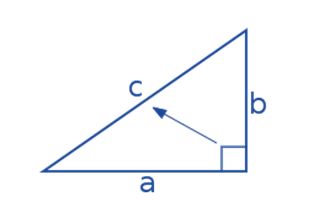
Di dalam segitiga siku-siku, ada tiga sisi: dua sisi yang lebih pendek disebut "sisi kaki" (a dan b), dan sisi terpanjang yang berseberangan dengan sudut 90 derajat disebut "sisi miring" atau "hipotenusa" (c).
Prinsip yang diungkapkan oleh rumus Pythagoras adalah bahwa kuadrat dari panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat dari panjang sisi kaki. Ini berlaku hanya untuk segitiga siku-siku dan merupakan dasar bagi banyak konsep dalam geometri dan matematika lebih lanjut.
Rumus Pythagoras memiliki aplikasi luas dalam berbagai bidang, termasuk fisika, astronomi, rekayasa, dan lain-lain. Ilmu ini digunakan untuk menghitung jarak, kecepatan, dan berbagai hubungan trigonometri dalam konteks segitiga siku-siku. Dengan menggunakan rumus Pythagoras, kita dapat memahami dan menghitung berbagai properti geometris serta hubungan antara panjang sisi dalam segitiga siku-siku.
Cara menghitung rumus phytagoras.
foto: istimewa
Rumus Pythagoras digunakan untuk menghitung panjang sisi miring (hipotenusa) dari sebuah segitiga siku-siku jika panjang kedua sisi kaki diketahui. Berikut adalah langkah-langkah untuk menghitung menggunakan rumus Pythagoras:
Langkah 1: Identifikasi Sisi-Sisi Segitiga
Tentukan sisi-sisi mana yang merupakan sisi kaki (a dan b) dan sisi mana yang merupakan hipotenusa (c) dalam segitiga siku-siku. Hipotenusa adalah sisi yang berseberangan dengan sudut 90 derajat.
Langkah 2: Tulis Rumus Pythagoras
Tuliskan rumus Pythagoras dengan memasukkan panjang sisi kaki ke dalam rumus:
C2 = a2 + b2
Langkah 3: Substitusi dan Perhitungan
Substitusi nilai panjang sisi kaki (a dan b) yang diketahui ke dalam rumus. Kemudian hitung kuadrat dari panjang sisi kaki, jumlahkan kedua kuadrat tersebut, dan ambil akar kuadratnya untuk mendapatkan panjang hipotenusa (c).
Langkah 4: Hitung Hasil Akhir
Hitung hasil akhir dengan mengambil akar kuadrat dari hasil penjumlahan kuadrat panjang sisi kaki:
C= √(a2 + b2 )
Ciri-ciri rumus Pythagoras.
foto: pexels.com
1. Berlaku hanya untuk segitiga siku-siku:
Rumus Pythagoras hanya berlaku untuk segitiga siku-siku, yaitu segitiga yang memiliki satu sudut tepat (90 derajat).
2. Hubungan antara panjang sisi-sisi:
Rumus Pythagoras menghubungkan panjang sisi-sisi segitiga siku-siku. Dalam segitiga tersebut, panjang sisi kaki (a dan b) dan panjang sisi miring (c) memiliki hubungan matematika tertentu.
3. Bentuk persamaan kuadrat:
Rumus Pythagoras dinyatakan dalam bentuk persamaan kuadrat:
C2 = a2 + b2
4. Penerapan dalam teorema pythagoras:
Rumus Pythagoras merupakan inti dari Teorema Pythagoras, yang menyatakan bahwa kuadrat dari panjang sisi miring (hipotenusa) segitiga siku-siku sama dengan jumlah kuadrat panjang sisi kaki.
5. Berfungsi untuk menghitung panjang sisi miring:
Salah satu ciri utama rumus Pythagoras adalah bahwa ia digunakan untuk menghitung panjang sisi miring (hipotenusa) segitiga siku-siku ketika panjang kedua sisi kaki diketahui.
6. Menggunakan operasi aritmatika:
Rumus Pythagoras melibatkan operasi aritmatika, yaitu penghitungan pangkat dua (kuadrat), penjumlahan, dan akar kuadrat.
7. Bersifat umum dan fundamental:
Rumus Pythagoras merupakan salah satu konsep dasar dalam matematika dan geometri, yang memiliki aplikasi luas dalam berbagai bidang ilmu dan kehidupan sehari-hari.
8. Menghubungkan konsep trigonometri:
Rumus Pythagoras juga memiliki kaitan dengan konsep trigonometri, khususnya dalam hubungan antara panjang sisi dalam segitiga siku-siku dengan sudut-sudutnya.
Recommended By Editor
- Rumus luas lingkaran lengkap dengan pengertian dan contoh soalnya
- Rumus volume tabung lengkap dengan pengertian, ciri, dan jenisnya
- Pengertian luas trapesium yang lengkap dengan ciri dan fungsinya
- 9 Trik cerdas matematika ini nggak diajarkan di sekolah, bikin kamu bisa berhitung tanpa kalkulator
- Aksi guru SD ajarkan matematika dengan cara unik ini viral, warganet puji kreativitasnya
- 13 Contoh soal himpunan dan jawaban, mudah banget










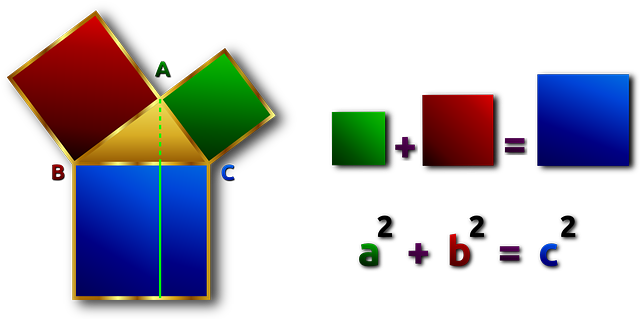

















![[KUIS] Kalau alat tukang bisa diubah jadi perabot, kira-kira kamu ingin mengubah yang mana?](https://cdn-brilio-net.akamaized.net/webp/news/2024/11/25/312761/30x30-kuis-kalau-alat-tukang-bisa-diubah-jadi-perabot-kira-kira-kamu-ingin-mengubah-yang-mana-2411250.jpg)


![[KUIS] Kalau kamu punya sepeda, kira-kira cocoknya jadi penjual apa? Cari tahu jawabannya di sini](https://cdn-brilio-net.akamaized.net/webp/news/2024/11/25/312757/30x30-kuis-kalau-kamu-punya-sepeda-kira-kira-cocoknya-jadi-penjual-apa-cari-tahu-jawabannya-di-sini-2411254.jpg)


![[KUIS] Pilih driver ojek online andalanmu dan temukan kata-kata bijak yang bisa mewarnai harimu](https://cdn-brilio-net.akamaized.net/webp/news/2024/11/25/312750/30x30-kuis-pilih-driver-ojek-online-andalanmu-dan-temukan-kata-kata-bijak-yang-bisa-mewarnai-harimu-2411253.jpg)

















