Rumus belah ketupat dalam matematika, pengertian, contoh soal dan cara mudah mengerjakannya

Brilio.net - Dalam matematika, saat sudah sampai pada bab bangun datar, rumus belah ketupat adalah satu yang familiar. Pasalnya, bangun datar ini diajarkan sejak seseorang masih menempuh pendidikan Sekolah Dasar (SD).

Belah ketupat sendiri merupakan bentuk yang sangat sering ditemui dalam kehidupan sehari-hari. Apalagi buat kamu yang Muslim, setiap hari Raya Idul Fitri, di rumahmu selalu membuat ketupat yang bentuknya memang sangat persis dengan bangun datar belah ketupat yang dipelajari di sekolah.

Tahukah kamu tentang rumus belah ketupat? dalam pelajaran Matematika tepatnya di materi bangun geometri, rumus belah ketupat adalah sebuah rumus untuk bangun datar belah ketupat yang terdiri dari sebuah segi empat, dengan sisi-sisinya yang punya panjang, serta memiliki sudut sebesar 90 derajat.

Nah, untuk menghitung bangun datar yang memiliki sifat khusus ini, kamu tentu membutuhkan rumus belah ketupat untuk menghitung keliling, luas, serta diagonal-belahan.

Kali ini kamu akan menyimak penjelasan tentang rumus belah ketupat secara lengkap. Kalau kamu sedang kesulitan memahami rumus belah ketupat, mungkin kamu bisa menyimak dengan baik artikel berikut ini.

Dihimpun dari brilio.net dari berbagai sumber pada Selasa (31/10), berikut penjelasan lengkap tentang rumus belah ketupat dalam matematika, pengertian, contoh soal dan cara mudah mengerjakannya.

Pengertian Belah Ketupat

Belah ketupat adalah sebuah bentuk geometri dua dimensi yang terdiri dari sebuah segi empat dengan keempat sisinya memiliki panjang yang sama dan memiliki sudut di dalamnya sebesar 90 derajat. Dengan sifat-sifat khusus ini, belah ketupat dapat diidentifikasi berdasarkan keempat sisinya yang sama panjang dan keberadaan sudut di dalamnya yang berukuran 90 derajat. Sifat-sifat ini menjadikan belah ketupat sebagai salah satu bentuk geometri yang mudah dikenali.

Salah satu karakteristik utama belah ketupat adalah memiliki dua pasang sisi sejajar yang sama panjang. Selain itu, keempat sudut di dalam belah ketupat masing-masing berukuran 90 derajat.

Sifat-sifat ini membuat belah ketupat menjadi bentuk geometri yang memungkinkan untuk diidentifikasi dengan mudah. Terlepas dari sifatnya yang memiliki keempat sisi sama panjang dan memiliki dua pasang sudut yang sama, belah ketupat juga dapat dibedakan dengan jelas dengan bentuk geometri lainnya berdasarkan konsep keempat sudutnya yang sebesar 90 derajat.

Bentuk belah ketupat sering digunakan dalam berbagai konteks, baik dalam matematika, arsitektur, atau dalam konteks geometri dalam kehidupan sehari-hari. Kegunaan belah ketupat tidak hanya terbatas pada sifat-sifat geometrisnya, tetapi juga dalam aplikasi dalam berbagai bidang, seperti pengecoran bangunan, desain mozaik, atau bahkan dalam membentuk suatu pola tertentu. Dengan sifat-sifatnya yang jelas dan sederhana, belah ketupat menjadi salah satu bentuk geometri yang sangat mudah dikenali dan digunakan dalam berbagai aspek kehidupan.

Rumus Belah Ketupat

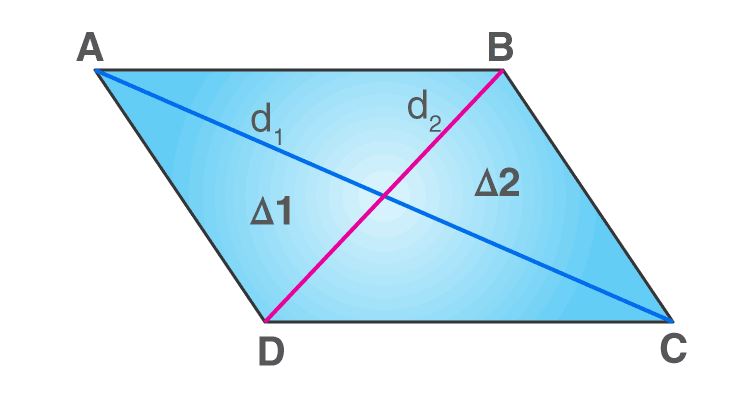
Rumus belah ketupat dalam matematika
byjus.com

1. Keliling Belah Ketupat:

Untuk kamu ingat, keliling belah ketupat adalah jumlah panjang keempat sisinya. Adapun rumusnya adalah sebagai berikut.

K = 4s

Catatan:
- K adalah keliling
- s adalah panjang sisi belah ketupat.

2. Luas Belah Ketupat:

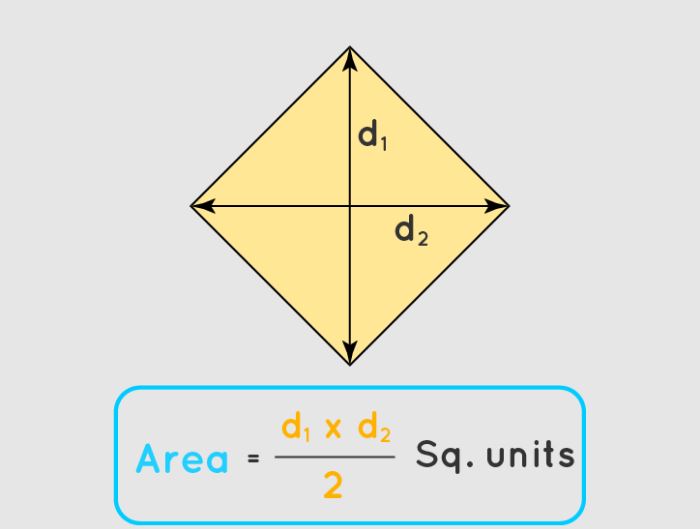
Luas belah ketupat dihitung sebagai separuh dari hasil perkalian dua diagonal-belahan.

A = (d1 x d2) : 2

Catatat:
- A adalah luas
- d1 serta d2 adalah diagonal-belahan belah ketupat.

Contoh Soal Rumus Belah KEtupat dan Cara Mudah Mengerjakannya

Contoh Soal 1:

Sebuah belah ketupat memiliki panjang sisi 6 cm. Hitunglah kelilingnya!

Pemecahan Soal:

Diketahui, s = 6 cm.

Menghitung Keliling:

Gunakan rumus K = 4s untuk menghitung keliling.
K = 4 x 6
K = 24 cm

Jadi, keliling belah ketupat adalah 24 cm.

Contoh Soal 2:

Sebuah belah ketupat memiliki keliling 32 cm. Jika panjang sisi belah ketupat adalah 8 cm, hitunglah luasnya!

Pemecahan Soal:

Diketahui, K = 32 cm dan s = 8 cm.

Mencari Luas:
Untuk mencari luas, pertama hitung panjang diagonal-belahan (d) menggunakan rumus d = K/4.

d = 32/4
d = 8 cm

Kemudian gunakan rumus belah ketupat A = (d1 x d2) : 2
untuk menghitung luas.

A = (8 x 8) : 2
A = 64/2
A = 32 cm

Jadi, luas belah ketupat tersebut adalah 32 cm.

Contoh Soal 3:

Sebuah belah ketupat memiliki luas 48 cm. Jika diagonal-belahan pertama 8 cm, hitunglah diagonal-belahan kedua!

Pemecahan Soal:

Diketahui, A = 48 cm dan d1 = 8 cm.

Mencari Diagonal-belahan Kedua:
Gunakan rumus luas A = (d1 x d2) : 2 untuk mencari (d2).

48 = (8 x d2) : 2
48 = 4d2
d2 = 48/4
d2 = 12 cm

Jadi, diagonal-belahan kedua belah ketupat adalah 12 cm.

Contoh Soal 4:

Sebuah belah ketupat memiliki keliling 40 cm. Hitunglah panjang diagonal-belahan jika panjang sisi belah ketupat adalah 10 cm.

Pemecahan Soal:

Diketahui, K = 40 cm dan s = 10 cm.

Mencari Panjang Diagonal-belahan:
Hitung panjang diagonal-belahan menggunakan rumus d = K/4.

d = 40/4
d = 10 cm

Jadi, panjang diagonal-belahan belah ketupat adalah 10 cm.

Contoh Soal 5:

Sebuah belah ketupat memiliki luas 64 cm. Jika diagonal-belahan pertama 12 cm, hitunglah keliling belah ketupat tersebut!

Pemecahan Soal:

Diberikan A = 64 cm dan d1 = 12 cm.

Mencari Keliling:
Gunakan rumus luas A = (d1 x d2) : 2 untuk mencari d2.

64 = (12 x d2) : 2
64 = 6d2
d2 = 64/6
d2 10.67 cm

Jadi, sekitar panjang diagonal-belahan kedua belah ketupat adalah sekitar 10.67 cm.

Tips Mudah Mengerjakan Soal Dengan Rumus Belah Ketupat

Rumus belah ketupat dalam matematika
cuemath.com

1. Pahami Sifat-sifat Belah Ketupat

Pastikan kamu memahami sifat-sifat belah ketupat seperti sisi-sisi yang sama panjang, sudut yang berdekatan 90 derajat, dan sifat diagonal-belahan.

2. Konsisten dengan Rumus

Pastikan untuk menggunakan rumus yang sesuai untuk perhitungan keliling, luas, dan diagonal-belahan. Perhatikan variabel yang diberikan dalam soal.

3. Langkah-langkah Sistematis

Jika memungkinkan, ikuti langkah-langkah secara sistematis. Misalnya, jika soal memberikan informasi keliling, gunakan rumus keliling untuk menghitung sisi dan seterusnya.

4. Perhatikan Perhitungan Diagonal-belahan

Perhitungan diagonal-belahan sering diperlukan dalam menyelesaikan soal belah ketupat, jadi pastikan perhitungannya benar.