Rumus dilatasi transformasi geometri lengkap dengan pengertian, karakteristik, dan contoh soal

Brilio.net - Saat mempelajari materi matematika pasti akan menemukan istilah translasi, refleksi, rotasi, dan dilatasi. Istilah dilatasi dapat dimaknai sebagai pengembangan, pemuaian, pembesaran, dan perkalian. Dilatasi adalah transformasi yang mengubah suatu ukuran (memperbesar atau memperkecil) suatu bangun geometri tanpa mengubah bentuk bangunnya.

Dilatasi transformasi geometri juga dikenal sebagai transformasi skala atau transformasi perbesaran atau pengencangan. Dilatasi dapat dilakukan dengan dua cara, yaitu dilatasi dengan faktor skala yang lebih besar dari 1 (dilatasi pengencangan) dan dilatasi dengan faktor skala lebih kecil dari satu (dilatasi perbesaran).

Nah, supaya kamu lebih memahami tentang dilatasi transformasi geometri, yuk simak rangkuman brilio.net tentang rumus dilatasi transformasi geometri lengkap dengan pengertian, karakteristik, dan contoh soal dari berbagai sumber pada Selasa (17/10).

Pengertian dan rumus dilatasi transformasi geometri.

rumus dilatasi transformasi geometri
Istimewa

Dilatasi transformasi geometri adalah suatu proses di mana sebuah objek atau gambar pada bidang euclidean diperbesar atau diperkecil tanpa mengubah bentuk atau orientasinya. Dilatasi dapat didefinisikan dengan menggunakan faktor skala yang merupakan faktor semua panjang sisi dan jarak antara titik-titik pada objek diperbesar atau diperkecil. Faktor skala ini dapat lebih besar dari 1 (dilatasi perbesaran) atau lebih kecil dari 1 (dilatasi pengencangan).

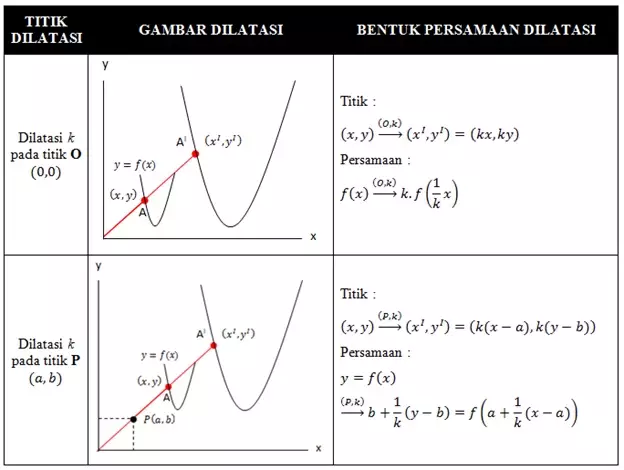
Secara umum, jika kita memiliki titik (x, y) di bidang, dilatasi dengan faktor skala k akan menghasilkan titik (kx, ky). Koordinat titik-titik pada objek dikali dengan faktor k untuk menghasilkan koordinat titik-titik pada objek yang sudah diperbesar atau diperkecil. Dilatasi dapat dilakukan terhadap titik tunggal, garis, objek 2D, atau objek 3D.

Rumus dilatasi dapat dinyatakan sebagai berikut:

1. Dilatasi dengan faktor skala k (k > 1):

- Untuk titik (x, y) di bidang kartesian, hasil dilatasi adalah (kx, ky).
- Jika Anda memiliki sebuah objek atau gambar dengan koordinat titik (x, y), dan Anda ingin menggandakan ukuran objek tersebut, Anda dapat mengalikan kedua koordinat x dan y dengan faktor k.

2. Dilatasi dengan faktor skala 1/k (0 < k < 1):

- Untuk titik (x, y) di bidang kartesian, hasil dilatasi adalah (x/k, y/k).
- Jika Anda ingin menyusutkan objek dengan faktor skala 1/k, Anda dapat membagi kedua koordinat x dan y dengan k.

Karakteristik dilatasi.

rumus dilatasi transformasi geometri
unsplash.com

Beberapa karakteristik dilatasi adalah sebagai berikut:

1. Sudut antara garis-garis yang melewati titik pusat dilatasi dan titik-titik objek tetap tidak berubah setelah dilatasi.
2. Luas objek diperbesar adalah k^2 kali luas objek asli jika faktor skala adalah k.
3. Garis-garis yang melewati titik pusat dilatasi diperpanjang atau diperkecil dengan faktor yang sama.
4. Jarak antara dua titik di objek dikali dengan faktor skala yang sama jika kedua titik tersebut memiliki jarak yang sama dengan titik pusat dilatasi.

Dilatasi sering digunakan dalam berbagai bidang, seperti matematika, fisika, desain grafis, dan memiliki banyak aplikasi yang bermanfaat dalam pemodelan, analisis, dan perancangan.

Contoh soal dilatasi transformasi geometri.

rumus dilatasi transformasi geometri
unsplash.com

1. Diberikan segitiga ABC dengan titik-titik koordinat A(2, 3), B(4, 1), dan C(5, 4). Lakukan dilatasi perbesaran dengan faktor skala 2 terhadap segitiga tersebut dan temukan koordinat dari titik-titik hasil dilatasi.

Pembahasan:
Dalam dilatasi perbesaran dengan faktor skala 2, kita akan menggandakan jarak antara titik-titik segitiga. Koordinat titik-titik hasil dilatasi adalah:

A'(2 x 2, 3 x 2) = A'(4, 6)
B'(4 x 2, 1 x 2) = B'(8, 2)
C'(5 x 2, 4 x 2) = C'(10, 8)

Jadi, koordinat titik-titik hasil dilatasi adalah A'(4, 6), B'(8, 2), dan C'(10, 8).

2. Anda memiliki sebuah persegi panjang dengan panjang 6 dan lebar 4. Lakukan dilatasi perkecilan dengan faktor skala 0.5 terhadap persegi panjang tersebut dan temukan panjang dan lebar dari hasil dilatasi.

Pembahasan:
Dalam dilatasi perkecilan dengan faktor skala 0.5, kita akan mengurangi panjang dan lebar asli menjadi setengah dari ukuran aslinya. Panjang dan lebar hasil dilatasi adalah:

Panjang: 6 x 0.5 = 3
Lebar: 4 x 0.5 = 2

Jadi, panjang dan lebar dari hasil dilatasi adalah 3 dan 2.

3. Diberikan titik A(1, 2) dan titik B(3, 4). Lakukan dilatasi perbesaran dengan faktor skala 3 terhadap garis yang melalui kedua titik tersebut dan temukan koordinat dari titik hasil dilatasi.

Pembahasan:
Dalam dilatasi perbesaran dengan faktor skala 3, kita akan menggandakan jarak antara kedua titik. Garis tersebut adalah garis yang melewati titik A dan B. Koordinat titik hasil dilatasi adalah:

A'(1 x 3, 2 x 3) = A'(3, 6)
B'(3 x 3, 4 x 3) = B'(9, 12)

Jadi, koordinat titik hasil dilatasi adalah A'(3, 6) dan B'(9, 12).

4. Anda memiliki sebuah lingkaran dengan jari-jari 5. Lakukan dilatasi perbesaran dengan faktor skala 1.5 terhadap lingkaran tersebut. Temukan jari-jari dari hasil dilatasi.

Pembahasan:
Dalam dilatasi perbesaran dengan faktor skala 1.5, jari-jari lingkaran akan diperbesar sebesar 1.5 kali. Jadi, jari-jari hasil dilatasi adalah:

Jari-jari: 5 x 1.5 = 7.5

Jadi, jari-jari dari hasil dilatasi adalah 7.5.

5. Diberikan segitiga ABC dengan titik-titik koordinat A(3, 1), B(5, 2), dan C(4, 4). Lakukan dilatasi perkecilan dengan faktor skala 0.75 terhadap segitiga tersebut dan temukan koordinat dari titik-titik hasil dilatasi.

Pembahasan:
Dalam dilatasi perkecilan dengan faktor skala 0.75, kita akan mengurangi jarak antara titik-titik segitiga menjadi 0.75 kali jarak aslinya. Koordinat titik-titik hasil dilatasi adalah:

A'(3 x 0.75, 1 x 0.75) = A'(2.25, 0.75)
B'(5 x 0.75, 2 x 0.75) = B'(3.75, 1.5)
C'(4 x 0.75, 4 x 0.75) = C'(3, 3)

Jadi, koordinat titik-titik hasil dilatasi adalah A'(2.25, 0.75), B'(3.75, 1.5), dan C'(3, 3).

6. Sebuah segitiga ABC memiliki panjang sisi AB = 6 cm, BC = 8 cm, dan CA = 10 cm. Dilatasi dengan faktor skala 2 dilakukan terhadap segitiga ini dengan titik pusat di A. Hitung panjang sisi segitiga yang baru (A'B', B'C', C'A') setelah dilatasi.

Pembahasan:
Faktor skala 2 berarti setiap panjang sisi segitiga yang baru akan menjadi dua kali lipat panjang sisi yang lama.

Sehingga, panjang sisi baru A'B' = 2 x 6 cm = 12 cm, B'C' = 2 x 8 cm = 16 cm, dan C'A' = 2 x 10 cm = 20 cm.

Jadi, panjang sisi segitiga yang baru adalah A'B' = 12 cm, B'C' = 16 cm, dan C'A' = 20 cm.

7. Sebuah persegi panjang memiliki panjang 12 cm dan lebar 6 cm. Dilatasi dilakukan dengan faktor skala 3 dengan titik pusat di tengah persegi panjang. Hitung panjang dan lebar dari persegi panjang yang baru.

Pembahasan:
Faktor skala 3 berarti setiap panjang sisi dari persegi panjang yang baru akan menjadi tiga kali lipat panjang sisi yang lama.

Panjang sisi baru = 3 x panjang sisi lama = 3 x 12 cm = 36 cm
Lebar sisi baru = 3 x lebar sisi lama = 3 x 6 cm = 18 cm

Jadi, panjang dan lebar dari persegi panjang yang baru adalah 36 cm dan 18 cm.

8. Sebuah lingkaran memiliki jari-jari 4 cm. Dilatasi dilakukan dengan faktor skala 1,5 dengan titik pusat di pusat lingkaran. Hitung jari-jari lingkaran yang baru.

Pembahasan:
Faktor skala 1,5 berarti jari-jari lingkaran yang baru akan menjadi 1,5 kali lipat jari-jari lingkaran yang lama.

Jari-jari lingkaran baru = 1,5 x jari-jari lingkaran lama = 1,5 x 4 cm = 6 cm

Jadi, jari-jari lingkaran yang baru adalah 6 cm.

9. Sebuah segitiga sama sisi memiliki panjang sisi 10 cm. Dilatasi dilakukan dengan faktor skala 0,5 dengan titik pusat di salah satu sudut segitiga. Hitung panjang sisi segitiga yang baru.

Pembahasan:
Faktor skala 0,5 berarti setiap panjang sisi segitiga yang baru akan menjadi setengah dari panjang sisi yang lama.

Panjang sisi baru = 0,5 x panjang sisi lama = 0,5 x 10 cm = 5 cm

Jadi, panjang sisi segitiga yang baru adalah 5 cm.

10. Sebuah persegi memiliki panjang sisi 8 cm. Dilatasi dilakukan dengan faktor skala 2 dengan titik pusat di salah satu sudut persegi. Hitung panjang sisi persegi yang baru.

Pembahasan:
Faktor skala 2 berarti setiap panjang sisi persegi yang baru akan menjadi dua kali lipat panjang sisi yang lama.

Panjang sisi baru = 2 x panjang sisi lama = 2 x 8 cm = 16 cm

Jadi, panjang sisi persegi yang baru adalah 16 cm.