Rumus gradien, beserta pengertian, contoh soal dan cara pengerjaannya

Brilio.net - Pernah nggak sih kamu mengamati kenapa tangga dibangun dengan presisi? Bila ditelusuri ternyata saat orang membuat tangga ada perhitungannya dalam matematika lho. Nah, untuk membangun tangga agar presisi maka diperlukan perhitungan dengan rumus gradien.

Secara sederhana rumus gradien adalah nilai yang menunjukkan kemiringan suatu garis lurus. Kenapa rumus kemiringan ini penting dalam membuat tangga? Bayangin deh saat pembangunan tangga asal-asalan tanpa mempertimbangkan kemiringannya, bisa jadi jarak antar tangga terlalu jauh.

Akibatnya apa? Yup, bisa mencelakai banyak orang termasuk kamu salah satunya. Oleh karena itu, penting banget mempelajari rumus gradien ini. Supaya lebih memahami rumus gradien ini, berikut brilio.net sajikan penjelasan lengkapnya mulai dari pengertian, sifat, contoh soal, dan cara pengerjaannya yang brilio.net himpun dari berbagai sumber pada Kamis (12/10).

Pengertian gradien dalam matematika.

foto: pexels.com

Gradien adalah bilangan yang menyatakan tingkat kemiringan suatu garis. Semakin miring suatu garis, semakin besar gradiennya. Untuk menentukan suatu gradien garis, kamu harus tahu dulu persamaan garisnya. Gradien dapat dilambangkan dengan huruf m dan dapat dicari dengan berbagai cara, tergantung pada informasi yang diketahui. Berikut adalah beberapa cara untuk mencari gradien:

- Jika diketahui persamaan garis lurus dalam bentuk y = mx + c, maka gradien adalah koefisien x, yaitu m. Contoh: jika y = 2x + 5, maka gradien adalah 2.

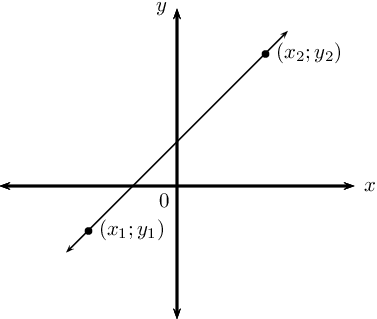
- Jika diketahui dua titik yang dilalui oleh garis lurus, misalnya (x1, y1) dan (x2, y2), maka gradien dapat dicari dengan rumus m = (y2 - y1) / (x2 - x1).

Contoh: jika garis lurus melalui titik (1, 3) dan (4, 7), maka gradien adalah (7 - 3) / (4 - 1) = 4/3.

- Jika diketahui satu titik yang dilalui oleh garis lurus dan gradien garis tersebut, misalnya (x1, y1) dan m, maka persamaan garis lurus dapat dicari dengan rumus y - y1 = m(x - x1).

Contoh: jika garis lurus memiliki gradien 3 dan melalui titik (2, 4), maka persamaan garis lurus adalah y - 4 = 3(x - 2).

- Rumus gradien dengan dua garis sejajar yang berarti garis A dan B saling sejajar. Dengan begitu, gradien kedua garis tersebut adalah sama. Ditulis dalam rumus:

mA = mB

- Rumus gradien dengan dua garis tegak lurus, ketika ada dua garis yang saling tegak lurus, maka hasil kali kedua gradiennya adalah -1. Ditulis dalam rumus:

mA x mB = -1

Sifat-sifat gradien.

foto: Istimewa

Dalam mempelajari rumus gradien, kamu harus memahami beberapa sifat gradien yang perlu diketahui, yaitu:

- Dua garis yang sejajar memiliki gradien yang sama. Contoh: jika garis A memiliki gradien 2 dan sejajar dengan garis B, maka garis B juga memiliki gradien 2.

- Dua garis yang tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Contoh: jika garis A memiliki gradien 3 dan tegak lurus dengan garis B, maka garis B memiliki gradien -1/3.

- Garis yang sejajar dengan sumbu x memiliki gradien nol. Contoh: jika garis C sejajar dengan sumbu x, maka gradien C adalah 0.

- Garis yang sejajar dengan sumbu y tidak memiliki gradien yang terdefinisi. Contoh: jika garis D sejajar dengan sumbu y, maka gradien D tidak dapat dicari.

Contoh soal rumus gradien dan penyelesaiannya.

foto: Istimewa

1. Jika diketahui persamaan garis y = 3x - 5, maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis adalah koefisien x dalam persamaan garis. Jadi, gradien garis y = 3x - 5 adalah 3.

2. Jika diketahui dua titik yang dilalui oleh garis lurus, yaitu A(2, 4) dan B(6, 8), maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis dapat dicari dengan rumus m = (y2 - y1) / (x2 - x1), dengan (x1, y1) dan (x2, y2) adalah dua titik yang dilalui oleh garis.

Jadi, gradien garis yang melalui A(2, 4) dan B(6, 8) adalah m = (8 - 4) / (6 - 2) = 1.

3. Jika diketahui satu titik yang dilalui oleh garis lurus dan gradien garis tersebut, yaitu C(-3, 5) dan m = -2, maka persamaan garis tersebut adalah ...

Jawaban:

Persamaan garis yang melalui satu titik dan memiliki gradien tertentu dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis dan m adalah gradien garis.

Jadi, persamaan garis yang melalui C(-3, 5) dan memiliki gradien -2 adalah y - 5 = -2(x + 3), atau setelah disederhanakan menjadi 2x + y + 1 = 0.

4. Dua garis sejajar memiliki gradien yang sama. Jika diketahui persamaan salah satu garis adalah y = 4x + 7, maka persamaan garis sejajar lainnya yang melalui titik D(1, -2) adalah ...

Jawaban:

Gradien garis sejajar sama dengan gradien garis yang diketahui, yaitu 4. Persamaan garis sejajar dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis sejajar dan m adalah gradien garis sejajar.

Jadi, persamaan garis sejajar yang melalui D(1, -2) adalah y + 2 = 4(x - 1), atau setelah disederhanakan menjadi 4x - y - 6 = 0.

5. Dua garis tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Jika diketahui persamaan salah satu garis adalah y = -3x + 2, maka persamaan garis tegak lurus lainnya yang melalui titik E(0, 0) adalah ...

Jawaban:

Gradien garis tegak lurus sama dengan kebalikan dan berlawanan tanda dari gradien garis yang diketahui. Jika gradien garis yang diketahui adalah -3, maka gradien garis tegak lurus adalah 1/3.

Persamaan garis tegak lurus dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis tegak lurus dan m adalah gradien garis tegak lurus.

Jadi, persamaan garis tegak lurus yang melalui E(0, 0) adalah y - 0 = (1/3)(x - 0), atau setelah disederhanakan menjadi x - 3y = 0.

Berikut adalah tambahan lima soal rumus gradien dan jawaban yang saya buat berdasarkan hasil pencarian web:

6. Jika diketahui persamaan garis y = -5x + 3, maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis adalah koefisien x dalam persamaan garis.
Jadi, gradien garis y = -5x + 3 adalah -5.

7. Jika diketahui dua titik yang dilalui oleh garis lurus, yaitu F(-2, 1) dan G(4, -3), maka gradien garis tersebut adalah …

Jawaban:

Gradien garis dapat dicari dengan rumus m = (y2 - y1) / (x2 - x1), dengan (x1, y1) dan (x2, y2) adalah dua titik yang dilalui oleh garis.

Jadi, gradien garis yang melalui F(-2, 1) dan G(4, -3) adalah m = (-3 - 1) / (4 + 2) = -2/3.

8. Jika diketahui satu titik yang dilalui oleh garis lurus dan gradien garis tersebut, yaitu H(3, -4) dan m = 1/2, maka persamaan garis tersebut adalah …

Jawaban:

Persamaan garis yang melalui satu titik dan memiliki gradien tertentu dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis dan m adalah gradien garis.

Jadi, persamaan garis yang melalui H(3, -4) dan memiliki gradien 1/2 adalah y + 4 = (1/2)(x - 3), atau setelah disederhanakan menjadi x - 2y - 11 = 0.

9. Dua garis sejajar memiliki gradien yang sama. Jika diketahui persamaan salah satu garis adalah y = -4x + 6, maka persamaan garis sejajar lainnya yang melalui titik I(-1, 2) adalah …

Jawaban:

Gradien garis sejajar sama dengan gradien garis yang diketahui, yaitu -4. Persamaan garis sejajar dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis sejajar dan m adalah gradien garis sejajar.

Jadi, persamaan garis sejajar yang melalui I(-1, 2) adalah y - 2 = -4(x + 1), atau setelah disederhanakan menjadi 4x + y + 6 = 0.

10. Dua garis tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Jika diketahui persamaan salah satu garis adalah y = x/3 + 2, maka persamaan garis tegak lurus lainnya yang melalui titik J(0, -3) adalah …

Jawaban:

Gradien garis tegak lurus sama dengan kebalikan dan berlawanan tanda dari gradien garis yang diketahui.

Jika gradien garis yang diketahui adalah x/3, maka gradien garis tegak lurus adalah -3/x. Persamaan garis tegak lurus dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis tegak lurus dan m adalah gradien garis tegak lurus.

Jadi, persamaan garis tegak lurus yang melalui J(0, -3) adalah y + 3 = (-3/x)(x - 0), atau setelah disederhanakan menjadi xy + 3x = 0.