Rumus gradien, beserta pengertian, contoh soal dan cara pengerjaannya

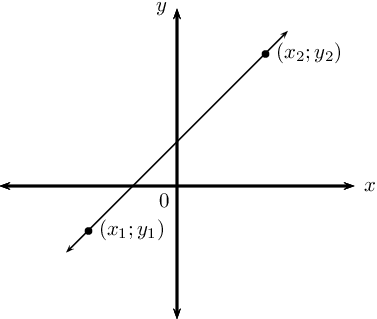
Sifat-sifat gradien.

foto: Istimewa

Dalam mempelajari rumus gradien, kamu harus memahami beberapa sifat gradien yang perlu diketahui, yaitu:

- Dua garis yang sejajar memiliki gradien yang sama. Contoh: jika garis A memiliki gradien 2 dan sejajar dengan garis B, maka garis B juga memiliki gradien 2.

- Dua garis yang tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Contoh: jika garis A memiliki gradien 3 dan tegak lurus dengan garis B, maka garis B memiliki gradien -1/3.

- Garis yang sejajar dengan sumbu x memiliki gradien nol. Contoh: jika garis C sejajar dengan sumbu x, maka gradien C adalah 0.

- Garis yang sejajar dengan sumbu y tidak memiliki gradien yang terdefinisi. Contoh: jika garis D sejajar dengan sumbu y, maka gradien D tidak dapat dicari.

Contoh soal rumus gradien dan penyelesaiannya.

foto: Istimewa

1. Jika diketahui persamaan garis y = 3x - 5, maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis adalah koefisien x dalam persamaan garis. Jadi, gradien garis y = 3x - 5 adalah 3.

2. Jika diketahui dua titik yang dilalui oleh garis lurus, yaitu A(2, 4) dan B(6, 8), maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis dapat dicari dengan rumus m = (y2 - y1) / (x2 - x1), dengan (x1, y1) dan (x2, y2) adalah dua titik yang dilalui oleh garis.

Jadi, gradien garis yang melalui A(2, 4) dan B(6, 8) adalah m = (8 - 4) / (6 - 2) = 1.

3. Jika diketahui satu titik yang dilalui oleh garis lurus dan gradien garis tersebut, yaitu C(-3, 5) dan m = -2, maka persamaan garis tersebut adalah ...

Jawaban:

Persamaan garis yang melalui satu titik dan memiliki gradien tertentu dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis dan m adalah gradien garis.

Jadi, persamaan garis yang melalui C(-3, 5) dan memiliki gradien -2 adalah y - 5 = -2(x + 3), atau setelah disederhanakan menjadi 2x + y + 1 = 0.

4. Dua garis sejajar memiliki gradien yang sama. Jika diketahui persamaan salah satu garis adalah y = 4x + 7, maka persamaan garis sejajar lainnya yang melalui titik D(1, -2) adalah ...

Jawaban:

Gradien garis sejajar sama dengan gradien garis yang diketahui, yaitu 4. Persamaan garis sejajar dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis sejajar dan m adalah gradien garis sejajar.

Jadi, persamaan garis sejajar yang melalui D(1, -2) adalah y + 2 = 4(x - 1), atau setelah disederhanakan menjadi 4x - y - 6 = 0.

5. Dua garis tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Jika diketahui persamaan salah satu garis adalah y = -3x + 2, maka persamaan garis tegak lurus lainnya yang melalui titik E(0, 0) adalah ...

Jawaban:

Gradien garis tegak lurus sama dengan kebalikan dan berlawanan tanda dari gradien garis yang diketahui. Jika gradien garis yang diketahui adalah -3, maka gradien garis tegak lurus adalah 1/3.

Persamaan garis tegak lurus dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis tegak lurus dan m adalah gradien garis tegak lurus.

Jadi, persamaan garis tegak lurus yang melalui E(0, 0) adalah y - 0 = (1/3)(x - 0), atau setelah disederhanakan menjadi x - 3y = 0.

Berikut adalah tambahan lima soal rumus gradien dan jawaban yang saya buat berdasarkan hasil pencarian web:

6. Jika diketahui persamaan garis y = -5x + 3, maka gradien garis tersebut adalah ...

Jawaban:

Gradien garis adalah koefisien x dalam persamaan garis.
Jadi, gradien garis y = -5x + 3 adalah -5.

7. Jika diketahui dua titik yang dilalui oleh garis lurus, yaitu F(-2, 1) dan G(4, -3), maka gradien garis tersebut adalah …

Jawaban:

Gradien garis dapat dicari dengan rumus m = (y2 - y1) / (x2 - x1), dengan (x1, y1) dan (x2, y2) adalah dua titik yang dilalui oleh garis.

Jadi, gradien garis yang melalui F(-2, 1) dan G(4, -3) adalah m = (-3 - 1) / (4 + 2) = -2/3.

8. Jika diketahui satu titik yang dilalui oleh garis lurus dan gradien garis tersebut, yaitu H(3, -4) dan m = 1/2, maka persamaan garis tersebut adalah …

Jawaban:

Persamaan garis yang melalui satu titik dan memiliki gradien tertentu dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis dan m adalah gradien garis.

Jadi, persamaan garis yang melalui H(3, -4) dan memiliki gradien 1/2 adalah y + 4 = (1/2)(x - 3), atau setelah disederhanakan menjadi x - 2y - 11 = 0.

9. Dua garis sejajar memiliki gradien yang sama. Jika diketahui persamaan salah satu garis adalah y = -4x + 6, maka persamaan garis sejajar lainnya yang melalui titik I(-1, 2) adalah …

Jawaban:

Gradien garis sejajar sama dengan gradien garis yang diketahui, yaitu -4. Persamaan garis sejajar dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis sejajar dan m adalah gradien garis sejajar.

Jadi, persamaan garis sejajar yang melalui I(-1, 2) adalah y - 2 = -4(x + 1), atau setelah disederhanakan menjadi 4x + y + 6 = 0.

10. Dua garis tegak lurus memiliki gradien yang merupakan kebalikan dan berlawanan tanda. Jika diketahui persamaan salah satu garis adalah y = x/3 + 2, maka persamaan garis tegak lurus lainnya yang melalui titik J(0, -3) adalah …

Jawaban:

Gradien garis tegak lurus sama dengan kebalikan dan berlawanan tanda dari gradien garis yang diketahui.

Jika gradien garis yang diketahui adalah x/3, maka gradien garis tegak lurus adalah -3/x. Persamaan garis tegak lurus dapat dicari dengan rumus y - y1 = m(x - x1), dengan (x1, y1) adalah titik yang dilalui oleh garis tegak lurus dan m adalah gradien garis tegak lurus.

Jadi, persamaan garis tegak lurus yang melalui J(0, -3) adalah y + 3 = (-3/x)(x - 0), atau setelah disederhanakan menjadi xy + 3x = 0.