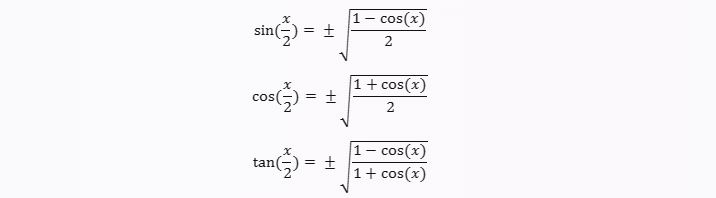Rumus identitas trigonometri, pahami pengertian, contoh soal, dan cara pengerjaannya

Rumus identitas trigonometri.

foto: freepik.com

Rumus identitas trigonometri adalah rumus yang menunjukkan kesamaan antara fungsi trigonometri yang berbeda. Rumus identitas trigonometri dapat digunakan untuk menyederhanakan atau mengubah ekspresi yang memuat fungsi trigonometri menjadi bentuk lain yang lebih mudah dihitung atau dianalisis.

Berikut adalah beberapa rumus identitas trigonometri yang umum digunakan:

1. Identitas trigonometri ganjil genap:

sin(x)= sin(x)

cos(x)= cos(x)

tan(x)= tan(x)

2. Identitas trigonometri kofungsi:

sin(/2 x)= cos(x)

cos(/2 x)= sin(x)

tan(/2 x)= cot(x)

3. Identitas trigonometri Pythagoras:

sin(x) + cos (x) = 1

1 + tan (x) = sec(x)

1 + cot (x) = csc(x)

4. Identitas trigonometri sudut ganda:

sin(2x) = 2sin(x) cos(x)

cos(2x)= cos(x)sin(x) = 1 2sin(x) = 2cos(x) 1

tan(2x)= 2tan(x)/ 1 tan(x)

5. Identitas trigonometri sudut tambah kurang:

sin(A + B) = sin(A) cos(B) + cos(A) sin(B)

sin(A B) = sin(A) cos(B) cos(A) sin(B)

cos(A + B) = cos(A) cos(B) sin(A)s in(B)

cos(A B) = cos(A) cos(B) + sin(A) sin(B)

tan(A + B) = 1 tan(A) tan(B) tan(A) + tan(B)

tan(A B) = 1 + tan(A) tan(B) tan(A) tan(B)

6. Identitas trigonometri sudut setengah:

foto: Istimewa

Contoh soal dan cara pengerjaan rumus identitas trigonometri.

foto: freepik.com

1. Buktikan bahwa sin(/4 + x) = 2/2(sinx + cosx).

Jawaban:

Dari identitas sin(A + B) = sinAcosB + cosAsinB, kamu bisa dapatkan:

Sin(/4 + x) = sin (/4)cos(x) + cos (/4)sin(x)

Karena sin (/4) = cos (/4) = 2/2, maka:

sin (/4 + x) = 2/2 cos(x) + 2/2 sin(x)

sin (/4 + x) = 2/2 (sinx + cosx)

Jadi, sin(/4 + x) = 2/2 (sinx + cosx) terbukti.

2. Sederhanakan ekspresi tan2(x)1.

Jawaban:

Dari identitas 1 + tan(x) = sec(x), kita dapatkan:

tan (x) - 1 = ( 1 + tan (x)) - 2

tan (x) - 1 = sec(x) - 2

Jadi, ekspresi tan(x) - 1 dapat disederhanakan menjadi sec(x) - 2

3. Tentukan nilai dari cos(3x) jika diketahui bahwa cos(6x) = 1/4.

Jawaban:

Dari identitas cos(3x) = 4cos(x) 3cos(x), kita dapatkan:

cos(6x) = 4cos(2x) - 3cos(2x)

Substitusikan cos(6x) = 1/4 = 1/2, maka:

1/4 = 4cos(2x) - 3cos(2x)

-1 = 16cos(2x) - 12cos(2x)

Faktorkan persamaan di atas, maka:

-1 = (4cos(2x) - 3)(4cos(2x) + 3cos(2x) + 1)

Untuk mendapatkan akar-akar real, kita harus memilih faktor yang bernilai nol, yaitu:

4cos(2x) - 3 = 0
cos(2x) = 3/4

Karena 0<6x<360, maka 0<2x<120. Dengan menggunakan kalkulator atau tabel trigonometri, kita dapat menentukan nilai x yang memenuhi persamaan di atas, yaitu:

x = 1/6 arccos(3/4) = 20,9

atau

x = 1/6(360 - arccos(3/4) = 79,0

Dengan demikian, nilai cos(3x) adalah:

cos(3x) = cos(3 x 20,9) = -0,5

Jadi, nilai cos(3x) adalah -0,5.

4. Nyatakan ekspresi sin(x)cot(x) ke dalam bentuk yang lebih sederhana.

Jawaban:

Dari definisi cot(x) = cos(x)/sin(x), dapat dijabarkan:

sin(x)cot(x) = sin(x).cos(x)/sin(x)

Sederhanakan pecahan diatas, maka:

sin(x)cot(x) = cos(x)