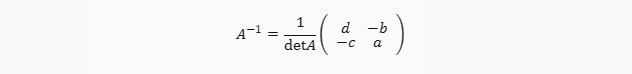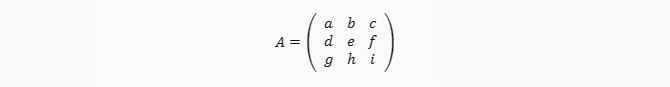Rumus invers matriks, pahami konsep, sifat, dan contoh soalnya

Rumus invers matriks.

foto: freepik.com

invers matriks adalah rumus yang digunakan untuk mencari matriks yang merupakan kebalikan dari matriks asal. Matriks yang merupakan kebalikan dari matriks asal disebut invers matriks. Invers matriks memiliki sifat bahwa jika dikalikan dengan matriks asal, hasilnya adalah matriks identitas. Matriks identitas adalah matriks yang memiliki angka 1 di diagonal utama dan angka 0 di luar diagonal utama.

Rumus invers matriks bergantung pada ordo atau ukuran matriks. Ordo matriks adalah jumlah baris dan kolom yang dimiliki oleh matriks. Baris adalah susunan angka secara horizontal, sedangkan kolom adalah susunan angka secara vertikal. Rumus invers matriks untuk ordo 2x2 dan 3x3 adalah sebagai berikut:

Rumus invers matriks ordo 2x2:

foto: Istimewa

A^1 adalah invers matriks A

detA adalah determinan matriks A, yaitu ad bc

a, b, c, dan d adalah elemen-elemen matriks A yang disusun sebagai berikut:

foto: Istimewa

Rumus ini didapatkan dengan menukar elemen diagonal utama, memberi tanda negatif pada elemen lain, dan membagi setiap elemen dengan determinan.

Rumus invers matriks ordo 3x3:

foto: Istimewa

Keteragan:

A^1 adalah invers matriks A

detA adalah determinan matriks A, yaitu a(ei fh)b(di fg) + c(dh eg)

a, b, c, , i adalah elemen-elemen matriks A yang disusun sebagai berikut:

foto: Istimewa

- Aij adalah kofaktor dari elemen aij, yaitu (1)^i+j dikali determinan minor dari elemen tersebut. Determinan minor adalah determinan yang didapatkan dengan menghilangkan baris dan kolom yang mengandung elemen tersebut.

- (.)^T adalah simbol untuk transpos, yaitu menukar baris dan kolom dari suatu matriks.

Rumus ini didapatkan dengan menghitung kofaktor dari setiap elemen, lalu mentranspos hasilnya.

Contoh soal rumus invers matriks dan jawabannya.

foto: freepik.com

Contoh soal 1

Berikan matriks A berikut:

A = | 2 1 |
| 4 3 |

Hitung matriks invers dari A.

Jawaban:

Untuk menghitung matriks invers A^(-1), kita perlu menggunakan rumus invers matriks. Pertama, kita hitung determinan matriks A:

det(A) = (2 * 3) - (1 * 4) = 6 - 4 = 2

Kemudian, kita hitung matriks adjoin dari A:

Adjoin(A) = | 3 -1 |
| -4 2 |

Akhirnya, kita hitung matriks invers A^(-1) dengan membagi matriks adjoin A dengan determinan A:

A^(-1) = (1/2) * Adjoin(A) = (1/2) * | 3 -1 |
| -4 2 |
= | 1.5 -0.5 |
| -2.0 1.0 |

Contoh soal 2

Berikan matriks B berikut:

B = | 5 1 |
| 2 4 |

Hitung matriks invers dari B.

Jawaban:

Sama seperti sebelumnya, kita mulai dengan menghitung determinan matriks B:

det(B) = (5 * 4) - (1 * 2) = 20 - 2 = 18

Kemudian, kita hitung matriks adjoin dari B:

Adjoin(B) = | 4 -1 |
| -2 5 |

Selanjutnya, kita hitung matriks invers B^(-1) dengan membagi matriks adjoin B dengan determinan B:

B^(-1) = (1/18) * Adjoin(B) = (1/18) * | 4 -1 |
| -2 5 |
= | 4/18 -1/18 |
| -2/18 5/18 |

Sederhana, kita bisa menyederhanakan matriks invers B:

B^(-1) = | 2/9 -1/18 |
| -1/9 5/18 |

Contoh soal 3

Berikan matriks C berikut:

C = | 3 1 |
| 6 2 |

Hitung matriks invers dari C.

Jawaban:

Langkah pertama adalah menghitung determinan matriks C:

det(C) = (3 * 2) - (1 * 6) = 6 - 6 = 0

Karena determinan C adalah 0, ini menunjukkan bahwa matriks C adalah matriks singular dan tidak memiliki invers. Jadi, matriks C^(-1) tidak dapat dihitung.