Rumus jajar genjang, lengkap dengan contoh soal dan penjelasan yang mudah dipahami

Brilio.net - Dalam matematika, kamu bakal mengenal berbagai bentuk bidang datar. Mulai dari persegi, persegi panjang, lingkaran, segitiga, trapesium dan jajar genjang. Bidang datar ini dibedakan dari bentuk yang menjadi ciri khasnya. Ada sisi-sisi yang membatasi bidang datar ini sehingga luas di dalamnya ataupun keliling bidang bisa diukur dengan rumus matematika.

Jajar genjang merupakan bidang datar yang menyerupai ketupat. Kalau kamu biasa melihat ketupat, artinya kamu sudah melihat bentuk jajar genjang dalam dunia nyata. Sama seperti bidang datar pada umumnya, jajar genjang juga memiliki berbagai rumus yang bisa digunakan untuk menghitung luas, sudut hingga kelilingnya.

Kalau kamu belajar matematika di sekolah, kamu pasti bakal belajar soal jajar genjang. Nah, untuk membantu kamu menyelesaikan soal yang berhubungan dengan jajar genjang, kamu bisa menyimak deretan rumus yang telah dihimpun brilio.net dari berbagai sumber, Jumat (1/9) berikut ini.

Pengertian jajar genjang.

foto: freepik.com

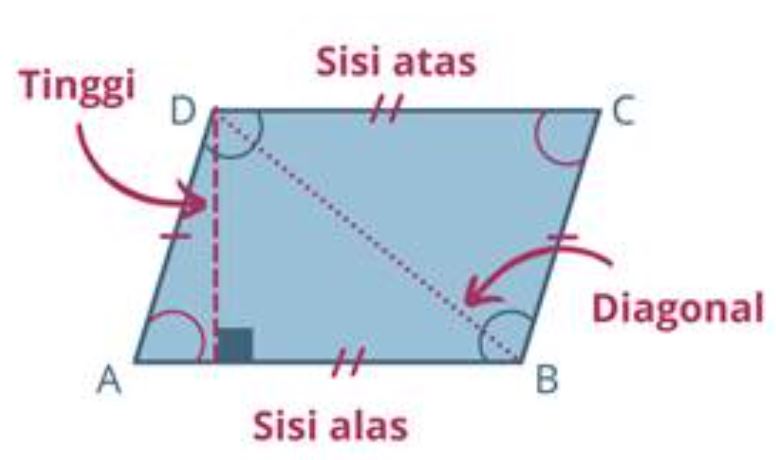
Jajar genjang adalah suatu bentuk bangun datar yang memiliki ciri-ciri utama berupa dua pasang sisi sejajar, dengan panjang yang sama dan sudut-sudut yang berhadapan juga memiliki ukuran yang sama. Dengan kata lain, jajar genjang adalah segi empat dengan dua pasang sisi sejajar, dan pasangan sudut yang berhadapan memiliki ukuran yang sama.

Ciri-ciri yang membedakan jajar genjang dari bentuk segi empat lainnya adalah adanya dua pasang sisi yang sejajar dan sudut yang berhadapan yang memiliki ukuran yang sama. Dua pasang sisi yang sejajar ini disebut "sisi sejajar," sedangkan dua sudut yang berhadapan dan memiliki ukuran yang sama disebut "sudut berhadapan."

Sifat jajar genjang:

1. Sisi sejajar.
Jajar genjang memiliki dua pasang sisi yang sejajar dengan panjang yang sama.

2. Sudut berhadapan.
Jajar genjang memiliki dua pasang sudut yang berhadapan dan memiliki ukuran yang sama.

3. Diagonal.
Jajar genjang memiliki dua diagonal yang saling memotong di titik tengah. Diagonal ini tidak hanya memotong pada titik tengah, tetapi juga membagi sudut berhadapan menjadi dua sudut yang sama besar.

4. Sifat sudut dalam.
Jumlah dari dua sudut dalam jajar genjang adalah 180 derajat, sama seperti segitiga.

5. Sifat Luas.
Luas jajar genjang dapat dihitung dengan mengalikan panjang alas dan tingginya.

 

Rumus jajar genjang.

foto: Istimewa

Rumus jajar genjang adalah kumpulan persamaan matematika yang digunakan untuk menghitung berbagai aspek dari jajar genjang, yaitu suatu jenis bangun datar yang memiliki dua pasang sisi sejajar dengan panjang yang sama dan sudut-sudut yang berhadapan juga memiliki ukuran yang sama.

Rumus jajar genjang:

1. Luas Jajar Genjang:

Luas = alas × tinggi

Luas = d1 × tinggi (d1 adalah salah satu diagonal)

Luas = d2 × tinggi (d2 adalah diagonal yang lain)

2. Keliling Jajar Genjang:

Keliling = 2 × (sisi sejajar pertama + sisi sejajar kedua)

Keliling = 2 × (a + b) (a dan b adalah panjang sisi sejajar)

3. Panjang Diagonal:

Diagonal d1 = √(a² + b² + 2ab × cos(α)) (α adalah sudut antara sisi sejajar pertama dan diagonal d1)

Diagonal d2 = √(a² + b² + 2ab × cos(β)) (β adalah sudut antara sisi sejajar pertama dan diagonal d2)

4. Tinggi Jajar Genjang:

Tinggi = d1 × sin(α) (α adalah sudut antara sisi sejajar pertama dan diagonal d1)

Tinggi = d2 × sin(β) (β adalah sudut antara sisi sejajar kedua dan diagonal d2)

Keterangan:
- "alas" mengacu pada panjang salah satu sisi pendek (jika menggunakan diagonal sebagai alas, bisa menggunakan panjang diagonal tersebut).

- "tinggi" adalah jarak antara sisi yang sejajar dan sejajar yang berhadapan.

- "sisi sejajar pertama" dan "sisi sejajar kedua" mengacu pada panjang sisi yang sejajar.

- "d1" dan "d2" adalah panjang kedua diagonal jajar genjang.

- "α" dan "β" adalah sudut yang relevan dalam jajar genjang.

Contoh soal rumus jajar genjang

foto: pexels.com

Soal 1

Dalam jajar genjang ABCD, panjang alas (AB) adalah 8 cm dan tinggi (h) adalah 5 cm. Hitunglah luas jajar genjang.

Penyelesaian:

Luas = alas × tinggi

Luas = 8 cm × 5 cm

Luas = 40 cm²

Soal 2

Sebuah jajar genjang memiliki panjang sisi sejajar pertama (AB) 12 cm dan panjang sisi sejajar kedua (CD) 9 cm. Berapakah keliling jajar genjang?

Penyelesaian:

Keliling = 2 × (sisi sejajar pertama + sisi sejajar kedua)

Keliling = 2 × (12 cm + 9 cm)

Keliling = 42 cm

Soal 3

Dalam jajar genjang ABCD, panjang sisi sejajar pertama (AB) adalah 10 cm dan tinggi (h) adalah 8 cm. Hitunglah luas jajar genjang.

Penyelesaian:

Luas = alas × tinggi

Luas = 10 cm × 8 cm

Luas = 80 cm²

Soal 4

Sebuah jajar genjang memiliki panjang diagonal pertama (d1) 7 cm dan panjang diagonal kedua (d2) 9 cm. Berapakah keliling jajar genjang?

Penyelesaian:

Keliling = 2 × (sisi sejajar pertama + sisi sejajar kedua)

Keliling = 2 × (d1 + d2)

Keliling = 2 × (7 cm + 9 cm)

Keliling = 32 cm

Soal 5

Dalam jajar genjang ABCD, panjang diagonal pertama (d1) adalah 10 cm dan panjang diagonal kedua (d2) adalah 8 cm. Sudut antara diagonal d1 dan d2 adalah 60 derajat. Hitunglah luas jajar genjang.

Penyelesaian:

Luas = ½ × d1 × d2 × sin(α) (α adalah sudut antara diagonal d1 dan d2)

Luas = ½ × 10 cm × 8 cm × sin(60°)

Luas = 20√3 cm²

Soal 6

Dalam jajar genjang ABCD, panjang sisi sejajar pertama (AB) adalah 16 cm dan panjang diagonal pertama (d1) adalah 12 cm. Berapakah panjang sisi sejajar kedua (CD)?

Penyelesaian:

Kita dapat menggunakan rumus Pythagoras untuk mencari panjang sisi sejajar kedua:

d1² = AB² + CD²

(12 cm)² = (16 cm)² + CD²

CD² = (12 cm)² - (16 cm)²

CD² = 144 cm² - 256 cm²

CD² = -112 cm²

Soal 7

Dalam jajar genjang ABCD, panjang sisi sejajar pertama (AB) adalah 14 cm dan sudut antara diagonal pertama (d1) dan sisi sejajar pertama adalah 45 derajat. Berapakah panjang diagonal pertama (d1)?

Penyelesaian:

d1 = AB / sin(α) (α adalah sudut antara d1 dan AB)

d1 = 14 cm / sin(45°)

d1 ≈ 19.80 cm

Soal 8

Dalam jajar genjang ABCD, panjang sisi sejajar pertama (AB) adalah 20 cm dan panjang diagonal pertama (d1) adalah 16 cm. Berapakah panjang sisi sejajar kedua (CD)?

Penyelesaian:

Kita dapat menggunakan rumus Pythagoras untuk mencari panjang sisi sejajar kedua:

d1² = AB² + CD²

(16 cm)² = (20 cm)² + CD²

CD² = (16 cm)² - (20 cm)²

CD² = 256 cm² - 400 cm²

CD² = -144 cm²

Soal 9

Dalam jajar genjang ABCD, panjang diagonal pertama (d1) adalah 15 cm dan panjang diagonal kedua (d2) adalah 12 cm. Sudut antara diagonal d1 dan d2 adalah 90 derajat. Hitunglah luas jajar genjang.

Penyelesaian:

Luas = ½ × d1 × d2 × sin(α) (α adalah sudut antara diagonal d1 dan d2)

Luas = ½ × 15 cm × 12 cm × sin(90°)

Luas = ½ × 15 cm × 12 cm × 1

Luas = 90 cm²

Soal 10

Dalam jajar genjang ABCD, panjang sisi sejajar pertama (AB) adalah 24 cm dan tinggi (h) adalah 10 cm. Hitunglah luas jajar genjang.

Penyelesaian:

Luas = alas × tinggi

Luas = 24 cm × 10 cm

Luas = 240 cm²

Soal 11

Sebuah jajar genjang memiliki panjang diagonal pertama (d1) 18 cm dan panjang diagonal kedua (d2) 12 cm. Berapakah keliling jajar genjang?

Penyelesaian:

Keliling = 2 × (sisi sejajar pertama + sisi sejajar kedua)

Keliling = 2 × (d1 + d2)

Keliling = 2 × (18 cm + 12 cm)

Keliling = 60 cm