Rumus keliling setengah lingkaran, pengertian, contoh soal, dan trik mudah mengerjakannya

Brilio.net - Salah satu bangun datar yang cukup populer dan jadi materi pelajaran wajib adalah lingkaran. Bangunan datar yang bentuknya bulat ini punya rumus tersendiri untuk mengidentifikasi beberapa ukuran seperti keliling, luas, ataupun mencari jari-jari.

Biasanya, kalau nggak paham betul konsep dan rumus lingkaran, soal matematika tentang materi ini pun akan terasa sulit saat mengerjakannya. Apalagi kalau kamu mendapatkan soal cerita yang terkesan mengecoh.

Oleh karena itu, rajin belajar dan menghafalkan rumus akan jadi cara agar kamu nggak kesulitan ketika mengerjakan soal ujian nanti. Nah, kali ini kamu akan dijelaskan mengenai rumus keliling setengah lingkaran.

Dirangkum brilio.net dari berbagai sumber pada Rabu (1/11), berikut ini penjelasan tentang rumus keliling setengah lingkaran, pengertian, contoh soal, dan trik mudah mengerjakannya. Cekidot!

Pengertian keliling setengah lingkaran.

foto: istimewa

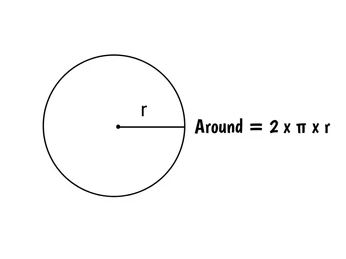
Rumus keliling setengah lingkaran adalah alat untuk mengukur total panjang lengkung setengah lingkaran. Diketahui, sebuah lingkaran dibagi menjadi dua bagian yang sama besar yang dikenal sebagai setengah lingkaran.

Keliling setengah lingkaran adalah panjang lengkung yang membentuk setengah lingkaran. Formula untuk menghitung keliling setengah lingkaran memang berhubungan langsung dengan menghitung panjang lengkung lingkaran.

Formula keliling setengah lingkaran.

foto: istimewa

Adapun rumus keliling setengah lingkaran dapat dihitung menggunakan rumus berikut:

K = π x r + 2r

Catatan :
- K adalah keliling setengah lingkaran
- π adalah konstanta yang hampir sama dengan 3,14159 atau 22/7 dan dapat disederhanakan menjadi 3,14
- r adalah jari-jari lingkaran

Contoh soal menggunakan rumus keliling setengah lingkaran.

foto: freepik.com

Contoh Soal 1:

Sebuah setengah lingkaran memiliki jari-jari sebesar 10 cm. Hitunglah keliling setengah lingkaran tersebut!

Pemecahan Soal:
Langkah pertama adalah menetapkan nilai yang diketahui dari soal. Diberikan bahwa r = 10 cm.

Langkah-langkahnya:
- Gunakan rumus K = π x r + 2r
- Masukkan nilai jari-jari r = 10 cm ke dalam rumus.

K = (3,14 x 10) + (2 x 10)
K = 31,4 + 20
K = 51,4 cm

Jadi, keliling setengah lingkaran dengan jari-jari 10 cm adalah sekitar 51,4159 cm.

Contoh Soal 2:

Jika keliling setengah lingkaran adalah 36π cm, tentukan panjang jari-jarinya!

Pemecahan Soal:
Diketahui nilai K = 36π cm. Kamu diminta untuk mencari nilai jari-jarinya (r).

Langkah-langkahnya:
- Diketahui rumus K = π x r + 2r
- Kamu diminta mencari (r).
- Kita substitusi nilai K = 36 π cm ke dalam rumus.

36π = π x r + 2r
36π = r (π + 2)
r = 36π/π + 2
r = 36 x 3,14/3,14 + 2

r ≈ 113,097/5,14
r ≈ 21,9999 cm

Jadi, panjang jari-jari setengah lingkaran tersebut adalah sekitar 22 cm.

Contoh Soal 3:

Sebuah taman memiliki sebuah jalan setapak berbentuk setengah lingkaran dengan jari-jari 15 meter. Berapakah keliling setengah lingkaran tersebut?

Pemecahan Soal:
Diketahui bahwa jari-jari (r) setengah lingkaran adalah 15 meter.

Langkah-langkahnya:
- Gunakan rumus keliling setengah lingkaran: K = π x r + 2r
- Masukkan nilai jari-jari r = 15 m ke dalam rumus.

K = 3,14 x 15 + 2 x 15
K = 47,1 + 30
K = 77,12385 m

Jadi, keliling setengah lingkaran dari jalan setapak tersebut adalah sekitar 77,12385 meter.

Contoh Soal 4:

Sebuah kolam renang memiliki bagian yang berbentuk setengah lingkaran dengan keliling 36π meter. Tentukan panjang jari-jari kolam renang tersebut.

Pemecahan Soal:
Diberikan bahwa keliling setengah lingkaran (K) adalah 36π meter. Nah, kamu diminta untuk mencari panjang jari-jarinya (r).

Langkah-langkahnya:
- Gunakan rumus keliling setengah lingkaran: K = π x r + 2r
- Kita diminta mencari (r)
- Ganti nilai (K) dengan (36π) meter.

36π = π x r + 2r
36π = r (π + 2)
r = 36π / π + 2
r = (36 x 3,14159) : (3,14159 + 2)
r ≈ 113,097 : 5,14159
r ≈ 21,9999 meter

Jadi, panjang jari-jari setengah lingkaran kolam renang tersebut adalah sekitar 22 meter.

Contoh Soal 5:

Sebuah arena olahraga memiliki sebuah lapangan bulu tangkis yang memiliki bentuk setengah lingkaran dengan keliling 42 meter. Berapakah panjang jari-jari lapangan bulu tangkis tersebut?

Pemecahan Soal:
Diberikan bahwa keliling setengah lingkaran (K) adalah 42 meter. Kita diminta untuk mencari panjang jari-jarinya (r).

Langkah-langkahnya:
- Gunakan rumus keliling setengah lingkaran: K = π x r + 2r
- Kita diminta mencari (r).
- Ganti nilai (K) dengan 42 meter.

42 = π x r + 2r
r (π + 2) = 42
r = 42 : (π + 2)
r = 42 : (3.14 + 2)
r ≈ 42 : 5,14
r ≈ 8,15 meter

Jadi, panjang jari-jari setengah lingkaran lapangan bulu tangkis tersebut adalah sekitar 8,15 meter.

Trik mudah mengerjakan rumus keliling setengah lingkaran.

foto: freepik.com

1. Pahami rumus.

Agar dapat menghitung keliling setengah lingkaran, sangat penting untuk memahami rumusnya dengan baik. Pahami hubungan antara π, jari-jari (r), dan langkah-langkah yang diperlukan.

2. Konsistensi satuan.

Pastikan untuk menggunakan satuan yang konsisten. Jika jari-jari diberikan dalam cm, pastikan keliling juga dalam satuan cm.

3. Perhatikan operasi matematika.

Ketika memecahkan soal, perhatikan operasi matematika yang dilakukan, terutama dalam menjaga presisi perhitungan nilai π. Pastikan nilai π diperlakukan secara akurat dalam perhitungan.

4. Gunakan pendekatan sederhana.

Dalam beberapa kasus, ketika nilai jari-jari diberikan, perhatikan kemungkinan menyederhanakan rumus untuk memudahkan perhitungan, terutama jika ada kemungkinan penggunaan nilai π sebagai 22/7 atau 3,14.

5. Langkah-langkah sistematis.

Saat menyelesaikan soal, langkah-langkahnya harus sistematis. Pastikan setiap langkah diikuti dengan benar dan tidak terburu-buru dalam melakukan perhitungan.

Kesimpulan.

Dengan memahami rumus keliling setengah lingkaran dan menerapkan trik mudah dalam mengerjakan soal, akan memudahkan kamu dalam menyelesaikan permasalahan terkait keliling setengah lingkaran dengan akurat. Selain itu, dengan pemahaman rumus keliling setengah lingkaran, kamu dapat menyelesaikan berbagai permasalahan terkait ukuran dan bentuk setengah lingkaran dengan tepat.