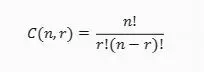Rumus kombinasi, lengkap dengan pengertian, contoh soal, dan cara pengerjaannya

Brilio.net - Stigma pelajaran matematika itu sulit, kini tidak relevan lagi. Pasalnya, dengan kecanggihan teknologi kamu bisa mempelajari apa saja termasuk rumus-rumus matematika. Salah satu sub bab materi matematika yang mudah dipelajari yaitu tentang rumus kombinasi.

Secara sederhana, rumus kombinasi merupakan cara menyusun objek tanpa memperhatikan urutan. Misalnya ada beberapa kelompok orang, untuk membagi kelompok tersebut kamu tidak perlu memperhatikan urutan orang tersebut. Tetapi kami bisa membagi secara acak. Contohnya A-B, A-C, B-C, dan lainnya.

Nah, berikut penjelasan lengkap tentang rumus kombinasi, lengkap dengan pengertian, contoh soal, dan cara pengerjaannya. Brilio.net menghimpun dari berbagai sumber pada Jumat (6/10).

Pengertian rumus kombinasi.

foto: freepik.com

Kombinasi adalah cara menyusun objek tanpa memperhatikan urutan, beda dengan permutasi yang penyusunannya harus berdasarkan urutan. Susunan {A,B} dan {B,A} dalam kombinasi disebut sama karena tidak mementingkan urutan. Namun dalam permutasi, urutan merupakan hal yang penting sehingga susunan {A,B} dan {B,A} disebut berbeda.

Rumus kombinasi adalah suatu persamaan yang digunakan untuk menentukan banyak cara menyusun atau memilih obyek. Rumus kombinasi dapat ditulis dengan notasi C(n,r) atau (nr), yang artinya banyak cara memilih r obyek dari n obyek tanpa menghiraukan urutan. Rumus kombinasi adalah:

foto: Istimewa

C(n,r) = n!/r!(n-r)!

Keterangan:
n! adalah faktorial dari n, yaitu hasil perkalian dari 1 sampai n
n adalah banyak obyek yang tersedia
r adalah banyak obyek yang dipilih atau disusun

Supaya lebih mengerti, cobalah pahami ilustrasi ini. Misalnya terdapat pengambilan 1 buku biru, 1 buku biru, dan 1 buku merah dari beberapa buku yang disediakan, sama dengan pengambilan 1 buku biru, 1 buku merah, dan 1 buku biru. Dimana ketika pengambilan buku yang terjadi adalah mendapat 2 buku biru dan 1 buku merah.

Ketika dihitung dalam rumus kombinasi maka digunakan operasi notasi faktorial (!). Operasi notasi faktorial dilakukan dengan mengalikan bilangan-bilangan asli dari bilangan terbesar sampai satu. Contoh notasi 6! adalah 6 x 5 x 4 x 3 x 2 x 1 = 720

Contoh soal rumus kombinasi dan penyelesaiannya.

foto: freepik.com

Contoh 1

Berapa banyak cara yang berbeda untuk memilih 2 buah buku dari 5 buah buku yang ada di perpustakaan?

Penyelesaian:
Untuk menyelesaikan masalah ini, kamu dapat menggunakan rumus kombinasi. Rumus kombinasi adalah C(n, k) = n! / (k!(n-k)!), di mana n adalah jumlah elemen yang dimiliki dan k adalah jumlah elemen yang ingin dipilih.

C(5, 2) = 5! / (2!(5-2)!)
C(5, 2) = (5 x 4) / (2 x 1)
C(5, 2) = 10

Jadi, ada 10 cara yang berbeda untuk memilih 2 buku dari 5 buku yang ada di perpustakaan.

Contoh 2

Sebuah tim sepak bola terdiri dari 11 pemain dan kita ingin memilih 3 pemain untuk menjadi kapten. Berapa banyak cara yang mungkin untuk memilih kapten?

Penyelesaian:
Karena kita hanya ingin memilih 1 kapten dari 11 pemain, kita dapat menggunakan rumus kombinasi sebagai berikut:

C(11, 1) = 11! / (1!(11-1)!)
C(11, 1) = 11

Jadi, ada 11 cara yang berbeda untuk memilih 1 kapten dari 11 pemain.

Contoh 3

Dalam sebuah kelompok musik, terdapat 4 anggota yang ingin menyusun susunan vokal mereka. Berapa banyak cara yang mungkin untuk menyusun susunan vokal?

Penyelesaian:
Kita ingin menyusun susunan vokal dari 4 anggota, jadi kita dapat menggunakan rumus kombinasi berikut:

C(4, 4) = 4! / (4!(4-4)!)
C(4, 4) = 4! / (4! x 0!)
C(4, 4) = 1

Jadi, ada hanya 1 cara yang mungkin untuk menyusun susunan vokal dari 4 anggota.

Contoh 4

Seorang guru memiliki 7 buah buku matematika dan ingin memilih 5 buku untuk digunakan dalam kelasnya. Berapa banyak cara yang mungkin untuk memilih buku-buku tersebut?

Penyelesaian:
Kita ingin memilih 5 buku dari 7 buku yang tersedia, jadi kita dapat menggunakan rumus kombinasi berikut:

C(7, 5) = 7! / (5!(7-5)!)
C(7, 5) = 7! / (5! x 2!)
C(7, 5) = (7 x 6) / (2 x 1)
C(7, 5) = 21

Jadi, ada 21 cara yang berbeda untuk memilih 5 buku dari 7 buku matematika.

Contoh 5

Seorang pemain catur memiliki 8 jenis pion yang berbeda. Berapa banyak cara yang mungkin untuk memilih 3 pion untuk digunakan dalam permainan catur?

Penyelesaian:
Kita ingin memilih 3 pion dari 8 jenis yang berbeda, jadi kita dapat menggunakan rumus kombinasi berikut:

C(8, 3) = 8! / (3!(8-3)!)
C(8, 3) = 8! / (3! x 5!)
C(8, 3) = (8 x 7 x 6) / (3 x 2 x 1)
C(8, 3) = 56

Jadi, ada 56 cara yang berbeda untuk memilih 3 pion dari 8 jenis yang berbeda dalam permainan catur.

Contoh 6

Sebuah restoran memiliki menu dengan 10 hidangan utama yang berbeda. Jika seorang pelanggan ingin memesan 3 hidangan utama untuk makan malam, berapa banyak cara yang mungkin untuk memesan hidangan-hidangan tersebut?

Penyelesaian:
Kita ingin memilih 3 hidangan utama dari 10 yang berbeda, jadi kita dapat menggunakan rumus kombinasi berikut:

C(10, 3) = 10! / (3!(10-3)!)
C(10, 3) = 10! / (3! x 7!)
C(10, 3) = (10 x 9 x 8) / (3 x 2 x 1)
C(10, 3) = 120

Jadi, ada 120 cara yang berbeda untuk memesan 3 hidangan utama dari menu tersebut.

Contoh 7

Seorang guru memiliki 12 murid di kelasnya dan ingin memilih sebuah tim dengan 4 murid untuk mengerjakan proyek bersama. Berapa banyak cara yang mungkin untuk membentuk tim proyek?

Penyelesaian:
Kita ingin memilih 4 murid dari 12 murid yang ada di kelas, jadi kita dapat menggunakan rumus kombinasi berikut:

C(12, 4) = 12! / (4!(12-4)!)
C(12, 4) = 12! / (4! x 8!)
C(12, 4) = (12 x 11 x 10 x 9) / (4 x 3 x 2 x 1)
C(12, 4) = 495

Jadi, ada 495 cara yang berbeda untuk membentuk tim proyek dengan 4 murid dari 12 murid.

Contoh 8

Sebuah toko bunga memiliki 6 jenis bunga yang berbeda, dan seorang pelanggan ingin membeli karangan bunga dengan 2 jenis bunga yang berbeda. Berapa banyak cara yang mungkin untuk memilih kombinasi bunga tersebut?

Penyelesaian:
Kita ingin memilih 2 jenis bunga dari 6 jenis yang berbeda, jadi kita dapat menggunakan rumus kombinasi berikut:

C(6, 2) = 6! / (2!(6-2)!)
C(6, 2) = 6! / (2! x 4!)
C(6, 2) = (6 x 5) / (2 x 1)
C(6, 2) = 15

Jadi, ada 15 cara yang berbeda untuk memilih kombinasi bunga tersebut.

Contoh 9

Sebuah tim olahraga memiliki 15 anggota, dan mereka ingin memilih 5 anggota untuk menjadi bagian dari tim inti yang akan bermain dalam pertandingan. Berapa banyak cara yang mungkin untuk memilih tim inti?

Penyelesaian:
Kita ingin memilih 5 anggota dari 15 anggota yang ada, jadi kita dapat menggunakan rumus kombinasi berikut:

C(15, 5) = 15! / (5!(15-5)!)
C(15, 5) = 15! / (5! x 10!)
C(15, 5) = (15 x 14 x 13 x 12 x 11) / (5 x 4 x 3 x 2 x 1)
C(15, 5) = 3,003

Jadi, ada 3,003 cara yang berbeda untuk memilih tim inti dari 15 anggota tersebut.

Contoh 10

Seorang siswa memiliki 8 pelajaran yang berbeda yang harus diajukan dalam jadwal kuliahnya. Dia ingin memilih 4 pelajaran untuk semester ini. Berapa banyak cara yang mungkin untuk memilih pelajaran-pelajaran tersebut?

Penyelesaian:
Kita ingin memilih 4 pelajaran dari 8 pelajaran yang berbeda, jadi kita dapat menggunakan rumus kombinasi berikut:

C(8, 4) = 8! / (4!(8-4)!)
C(8, 4) = 8! / (4! x 4!)
C(8, 4) = (8 x 7 x 6 x 5) / (4 x 3 x 2 x 1)
C(8, 4) = 70

Jadi, ada 70 cara yang berbeda untuk memilih 4 pelajaran untuk semester ini.