Rumus luas alas tabung, lengkap dengan contoh dan penyelesaiannya

Brilio.net - Sebagian orang menganggap matematika merupakan pelajaran yang susah untuk dipelajari. Pasalnya, rumus-rumusnya memang terkesan rumit dan harus dihitung dengan teliti. Apabila salah satu angka saja, maka semua hasilnya akan keliru. Meski begitu, nggak semua rumus matematika itu rumit, lho.

Terdapat beberapa materi matematika yang mudah dipahami. Salah satunya rumus luas alas tabung. Mencari nilai alas tabung tidak sesulit yang dibayangkan. Jika kamu ingin mempelajarinya supaya bisa mengerjakan soal-soal tabung yang diberikan, wajib banget simak penjelasan rumus luas alas tabung berikut.

Nah, berikut rumus luas alas tabung, lengkap dengan contoh dan penyelesaiannya, dihimpun brilio.net dari berbagai sumber, Kamis (31/8).

Pengertian luas alas tabung.

foto: Istimewa

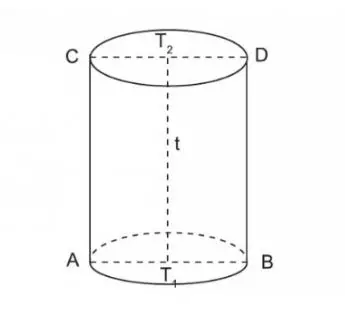
Alas tabung adalah permukaan datar dan melingkar yang menjadi dasar dari sebuah tabung. Tabung adalah objek tiga dimensi yang memiliki dua permukaan melingkar yang identik, disebut tutup atas dan tutup bawah, serta permukaan melengkung yang menghubungkan kedua tutup tersebut. Jadi, alas tabung adalah permukaan datar yang melingkar di bagian bawah tabung dan mendukung struktur keseluruhan tabung tersebut.

Misalnya, jika kamu membayangkan botol air mineral, alas tabungnya adalah permukaan datar pada bagian bawah botol yang menyentuh meja atau permukaan lainnya saat botol diletakkan tegak. Alas tabung ini biasanya berbentuk lingkaran, karena tutup dan permukaan melengkung pada bagian samping tabung adalah bagian dari bentuk tabung itu sendiri.

Dalam konteks matematika atau geometri, alas tabung sering dianggap sebagai lingkaran dengan jari-jari tertentu. Jika kamu ingin menghitung luas alas tabung, kamu bisa menggunakan rumus luas lingkaran (π x r²), di mana "r" adalah jari-jari lingkaran yang menjadi alas tabung.

Rumus luas alas tabung.

foto: Istimewa

Rumus untuk menghitung luas alas tabung adalah:

Luas Alas Tabung = π × r²

Keterangan:
- "π" (pi) adalah konstanta matematika yang memiliki perkiraan nilai 3.14159 atau lebih akurat tergantung pada kebutuhan perhitungan.

- "r" adalah jari-jari lingkaran yang menjadi alas tabung.

Dalam rumus ini, kita mengkuadratkan jari-jari lingkaran dan mengalikannya dengan nilai pi untuk mendapatkan luas alas tabung. Ini karena alas tabung berbentuk lingkaran, dan rumus luas lingkaran (π × r²) digunakan untuk menghitung luas permukaan alas yang datar ini.

Contoh soal dan penyelesaiannya.

foto: pexels.com

Soal 1

Sebuah tabung memiliki jari-jari alas sebesar 5 cm. Hitunglah luas alas tabung.

Penyelesaian:

Luas Alas Tabung = π × r²
Luas Alas Tabung = π × (5 cm)²
Luas Alas Tabung = π × 25 cm²
Luas Alas Tabung = 78.54 cm² (dengan mengambil π ≈ 3.14159)

Soal 2

Dalam tabung yang memiliki diameter alas 10 cm, berapakah luas alasnya?

Penyelesaian:

Diameter = 2 × Jari-jari
Jari-jari = Diameter / 2
Jari-jari = 10 cm / 2 = 5 cm

Luas Alas Tabung = π × r²
Luas Alas Tabung = π × (5 cm)²
Luas Alas Tabung = π × 25 cm²
Luas Alas Tabung ≈ 78.54 cm²

Soal 3

Tabung memiliki jari-jari 8 cm. Jika π dianggap 3.14, berapakah luas alas tabung?

Penyelesaian:

Luas Alas Tabung = π × r²
Luas Alas Tabung = 3.14 × (8 cm)²
Luas Alas Tabung = 3.14 × 64 cm²
Luas Alas Tabung = 200.96 cm²

Soal 4

Sebuah tabung memiliki diameter alas 12 cm. Hitunglah luas alasnya dengan menggunakan π ≈ 3.14.

Penyelesaian:

Jari-jari = Diameter / 2
Jari-jari = 12 cm / 2 = 6 cm

Luas Alas Tabung = π × r²
Luas Alas Tabung = 3.14 × (6 cm)²
Luas Alas Tabung = 3.14 × 36 cm²
Luas Alas Tabung ≈ 113.04 cm²

Soal 5

Diberikan tabung dengan luas alas 154 cm² dan jari-jari alas 7 cm. Berapa nilai π yang mungkin digunakan?

Penyelesaian:

Luas Alas Tabung = π × r²
154 cm² = π × (7 cm)²
154 cm² = 49π cm²

Jadi, nilai π yang mungkin digunakan adalah π ≈ 3.1429.

Soal 6

Tabung memiliki luas alas 314 cm². Jika jari-jari alas adalah 5 cm, berapakah nilai π yang mungkin?

Penyelesaian:

Luas Alas Tabung = π × r²
314 cm² = π × (5 cm)²
314 cm² = 25π cm²

Jadi, nilai π yang mungkin digunakan adalah π ≈ 12.56.

foto: pexels.com

Soal 7

Sebuah kaleng memiliki luas alas 176 cm². Jika tinggi kaleng adalah 10 cm, berapakah jari-jari alasnya?

Penyelesaian:

Luas Alas Tabung = π × r²
176 cm² = π × r²
r² = 176 cm² / π
r² ≈ 56.08 cm²
r ≈ √56.08 cm
r ≈ 7.49 cm

Soal 8

Sebuah tabung memiliki tinggi 15 cm dan luas permukaan total 942 cm². Berapakah jari-jari alasnya?

Penyelesaian:

Luas Permukaan Tabung = 2πr² + 2πrh
942 cm² = 2πr² + 2πrh

Diberikan tinggi (h) = 15 cm
942 cm² = 2πr² + 2πr(15 cm)
942 cm² = 2πr(r + 15 cm)

Sekarang kita harus mencari r (jari-jari alas) yang memenuhi persamaan di atas. Ini mungkin memerlukan metode numerik atau persamaan kuadrat dengan menghitung akar kuadrat dari x:

πr² = 4.73
r² ≈ 4.73 / π
r ≈ √(4.73 / π)
r ≈ 1.09 cm

Jadi, jari-jari alas tabung ini adalah sekitar 1.09 cm.

Soal 9

Tabung memiliki jari-jari 9 cm dan tinggi 20 cm. Hitunglah luas permukaan totalnya.

Penyelesaian:

Luas Permukaan Tabung = 2πr² + 2πrh
Luas Permukaan Tabung = 2π(9 cm)² + 2π(9 cm)(20 cm)
Luas Permukaan Tabung = 2π(81 cm²) + 2π(180 cm²)
Luas Permukaan Tabung = 162π cm² + 360π cm²
Luas Permukaan Tabung = 522π cm² (mengambil π ≈ 3.14159)

Soal 10

Dalam tabung yang luas permukaan totalnya 400 cm² dan tingginya 10 cm, berapakah jari-jari alasnya?

Penyelesaian:

Kita memiliki rumus untuk luas permukaan tabung:
Luas Permukaan Tabung = 2πr² + 2πrh

Di sini, tinggi tabung (h) adalah 10 cm, dan luas permukaan total (L) adalah 400 cm². Kamu ingin mencari jari-jari alas (r).

Pertama, Gantikan nilai yang diketahui ke dalam rumus luas permukaan tabung:

400 cm² = 2πr² + 2π(10 cm)r

Lalu kedua, sederhanakan persamaan:
200 cm² = πr² + 20πr

Untuk menyederhanakannya kamu bisa mencoba untuk mengatasi persamaan ini sebagai persamaan kuadrat dalam r.

Ubah πr² menjadi "x":
200 = x + 20πx
200 = x(1 + 20π)

Kemudian mengisolasi x. Ingat bahwa x = πr². Jadi, kita memiliki:

x = 200 / (1 + 20π)

Selanjutnya hitung nilai x (πr²):
x ≈ 3.18 cm²

Terakhir, cari nilai r (jari-jari alas) dengan menghitung akar kuadrat dari x:
πr² = 3.18
r² ≈ 3.18 / π
r ≈ √(3.18 / π)
r ≈ 0.999 cm

Jadi, jari-jari alas tabung ini adalah sekitar 0.999 cm.