Rumus luas belahan bola, beserta pengertian, ciri, dan cara pengerjaannya

Brilio.net - Bentuk-bentuk geometri tidak hanya ada di buku matematika, tetapi juga di sekitar kita. Salah satu bentuk geometri yang paling umum dan menarik adalah bola. Bola bisa ditemukan di alam, seperti bumi, bulan, matahari, dan planet-planet lainnya. 

Bola memiliki karakteristik khusus yang membuatnya berbeda dari bentuk lainnya, seperti simetri sempurna, volume maksimum, dan luas permukaan minimum. Dalam matematika, tidak hanya dihitung rumus bola utuh tetapi dapat dihitung belahan bola atau setengah bola. 

Supaya kamu lebih memahami tentang luas belahan bola ini, yuk simak penjelasan lengkap rumus luas belahan bola, beserta pengertian, ciri, dan cara pengerjaannya. Dihimpun brilio.net dari berbagai sumber pada Kamis (12/10).

Pengertian dan rumus luas belahan bola.

foto: Istimewa

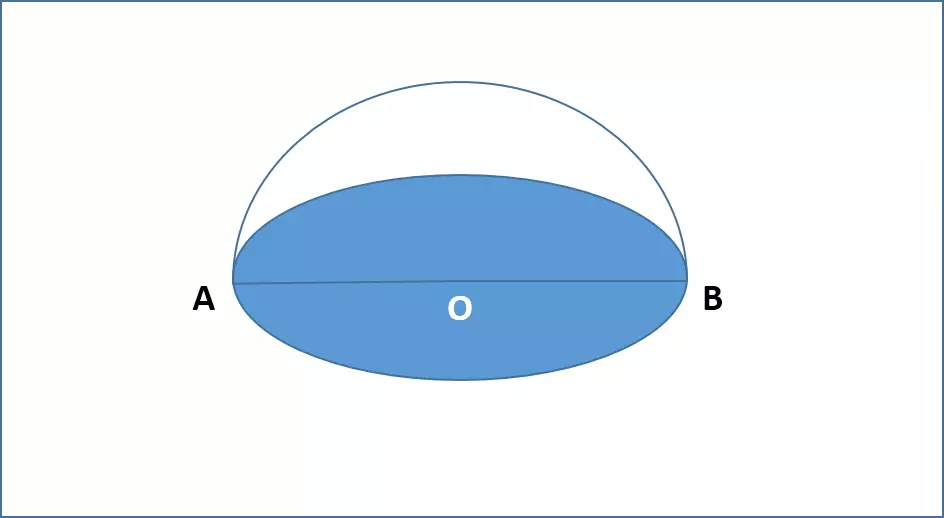
Belahan bola adalah bagian dari bola yang dibatasi oleh satu bidang datar yang memotong bola. Belahan bola memiliki jari-jari, pusat, dan luas permukaan yang sama dengan bola asalnya, tetapi volume yang setengah dari volume bola asalnya. Belahan bola juga disebut sebagai hemisfer atau setengah bola.

Rumus luas belahan bola.

Luas belahan bola = 1/2 x luas permukaan bola

Luas permukaan bola = 4 x π x r²

Jadi, luas belahan bola = 1/2 x 4 x π x r²

Luas belahan bola = 2 x π x r²

Ciri-ciri luas belahan bola.

foto: Istimewa

- Belahan bola adalah bagian dari bola yang dibatasi oleh satu bidang datar yang memotong bola.

- Belahan bola memiliki jari-jari, pusat, dan luas permukaan yang sama dengan bola asalnya, tetapi volume yang setengah dari volume bola asalnya.

- Belahan bola memiliki satu sisi lengkung dan satu sisi datar. Sisi lengkung disebut juga kulit belahan bola atau selimut belahan bola. Sisi datar disebut juga alas belahan bola atau irisan belahan bola.

- Belahan bola memiliki satu titik pusat yang berada di tengah-tengah sisi datar. Titik pusat ini juga merupakan titik pusat bola asalnya.

- Belahan bola memiliki jari-jari tak terhingga yang berawal dari titik pusat dan berakhir di sisi lengkung. Jari-jari ini juga merupakan jari-jari bola asalnya.

- Belahan bola memiliki diameter tak terhingga yang berawal dan berakhir di sisi lengkung. Diameter ini juga merupakan diameter bola asalnya.

Contoh soal luas belahan bola dan cara pengerjaannya.

foto: Istimewa

1. Jika jari-jari belahan bola adalah 6 cm, berapakah luas permukaan belahan bola tersebut? 

Jawab: 

Luas permukaan belahan bola = 2 x π x r² 

= 2 x π x 6²

= 72π cm².

2. Jika luas permukaan belahan bola adalah 50π cm^2, berapakah jari-jari belahan bola tersebut? 

Jawab: 

Luas permukaan belahan bola = 2 x π x r². 

Jadi, r² = luas permukaan belahan bola / (2 x π) 

= 50π / (2 x π) = 25. 

Jadi, r = akar(25) = 5 cm.

3. Jika jari-jari belahan bola adalah 10 cm, berapakah luas permukaan alas belahan bola tersebut? 

Jawab: 

Luas permukaan alas belahan bola adalah sama dengan luas lingkaran dengan jari-jari yang sama. 

Jadi, luas permukaan alas belahan bola = π x r² = π x 10² = 100π cm².

4. Jika luas permukaan alas belahan bola adalah 36π cm², berapakah jari-jari belahan bola tersebut? 

Jawab: 

Luas permukaan alas belahan bola = π x r². 

Jadi, r² = luas permukaan alas belahan bola / π = 36π / π = 36. Jadi, r = akar(36) = 6 cm.

5. Jika luas permukaan belahan bola adalah 200π cm² dan luas permukaan alas belahan bola adalah 100π cm², berapakah luas permukaan kulit belahan bola tersebut? 

Jawab: 

Luas permukaan kulit belahan bola adalah selisih antara luas permukaan belahan bola dan luas permukaan alas belahan bola. 

Jadi, luas permukaan kulit belahan bola = luas permukaan belahan bola - luas permukaan alas belahan bola = 200π - 100π = 100π cm².

6. Jika jari-jari belahan bola adalah 8 cm dan luas permukaan kulit belahan bola adalah 64π cm^2, berapakah luas permukaan belahan bola tersebut? 

Jawab: 

Luas permukaan belahan bola adalah jumlah antara luas permukaan kulit belahan bola dan luas permukaan alas belahan bola. 

Jadi, luas permukaan belahan bola = luas permukaan kulit belahan bola + luas permukaan alas belahan bola = 64π + π x r² 

= 64π + π x 8²

= 128π cm².

7. Jika jari-jari lingkaran yang menjadi alas sebuah topi ulang tahun adalah 7 cm dan tinggi topi ulang tahun tersebut adalah 21 cm, berapakah luas permukaan topi ulang tahun tersebut? 

Jawab: 

Topi ulang tahun dapat dianggap sebagai sebuah kerucut yang dibelah menjadi dua bagian yang sama besar. Jadi, luas permukaan topi ulang tahun adalah sama dengan luas permukaan setengah kerucut.

Luas permukaan setengah kerucut dapat dihitung dengan rumus: L = (1/4) x π x s x (s + r), di mana s adalah garis pelukis setengah kerucut. Untuk mencari s, dapat menggunakan teorema Pythagoras pada segitiga siku-siku yang terbentuk oleh tinggi, jari-jari, dan garis pelukis setengah kerucut. 

Jadi, s² = r² + t², di mana t adalah tinggi setengah kerucut. Karena tinggi setengah kerucut sama dengan setengah dari tinggi topi ulang tahun, maka t = (1/2) x h, di mana h adalah tinggi topi ulang tahun. 

Jadi, s² = r² + ((1/2) x h)². 

Substitusi nilai-nilai yang diketahui ke dalam rumus tersebut, kita dapatkan: s² = 7² + ((1/2) x 21)²

s² = 49 + (10,5)²

s² = 49 + 110,25

s² = 159,25

s = akar(159,25)

s ≈ 12,62 cm

Jadi, luas permukaan topi ulang tahun adalah:

L = (1/4) x π x s x (s + r)

L = (1/4) x π x 12,62 x (12,62 + 7)

L ≈ 154,67 cm²

8. Jika luas permukaan setengah bola pejal adalah 150π cm², berapakah jari-jari setengah bola tersebut? 

Jawab: Luas permukaan setengah bola pejal = 3 x π x r². 

Jadi, r² = luas permukaan setengah bola pejal / (3 x π) 

= 150π / (3 x π) = 50. 

Jadi, r = akar(50) = 5 akar(2) cm.

9. Jika jari-jari setengah bola berongga adalah 9 cm, berapakah luas permukaan setengah bola tersebut? 

Jawab: 

Luas permukaan setengah bola berongga = 2 x π x r² 

= 2 x π x 9²

= 162π cm².

10. Jika luas permukaan kulit setengah bola pejal adalah 75π cm² dan luas permukaan alas setengah bola pejal adalah 36π cm², berapakah jari-jari setengah bola pejal tersebut? 

Jawab: 

Luas permukaan setengah bola pejal adalah jumlah antara luas permukaan kulit setengah bola pejal dan luas permukaan alas setengah bola pejal. 

Jadi, luas permukaan setengah bola pejal = luas permukaan kulit setengah bola pejal + luas permukaan alas setengah bola pejal = 75π + 36π = 111π cm². 

Luas permukaan setengah bola pejal juga dapat dihitung dengan rumus: 

luas permukaan setengah bola pejal = 3 x π x r². 

Dengan menyamakan kedua persamaan tersebut, kita dapat menyelesaikan nilai r sebagai berikut: 

3 x π x r² = 111π. 

Jadi, r² = 111 / 3 = 37. 

Jadi, r = akar(37) cm.