Rumus luas jaring-jaring balok, beserta pengertian, ciri, dan contoh soalnya

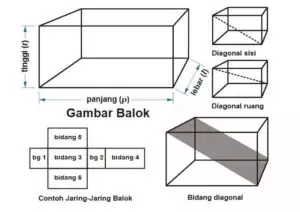
Brilio.net - Saat dibangku Sekolah Dasar kamu pasti pernah diperkenalkan dengan materi matematika tentang bentuk bangun ruang seperti balok. Balok mempunyai beberapa elemen yaitu tepi atau bidang, rusuk, titik sudut, bidang diagonal, diagonal spesial dan bidang diagonal.

Elemen-elemen balok itu akan membentuk jaring-jaring balok. Nah, kali ini kita akan mengupas tuntang rumus luas jaring-jaring balok. Jaring-jaring balok adalah bangun datar yang terdiri dari beberapa sisi yang dapat dilipat untuk membentuk balok. Selain itu, jaring-jaring balok juga memiliki beberapa variasi tergantung pada susunan sisi-sisinya.

Untuk menghitung luas jaring-jaring balok tidak terlalu rumit. Kamu hanya perlu memahami rumus luas jaring-jaring balok yaitu luas alas balok ditambah luas selubung balok kemudian dikalikan dengan dua.

Supaya kamu lebih mudah memahami tentang rumut luas jaring-jaring balok, berikut brilio.net mengulas rumus luas jaring-jaring balok, beserta pengertian, ciri, dan contoh soal yang mudah dipahami seperti dihimpun brilio.net dari berbagai sumber pada Selasa (3/10).

Pengertian jaring-jaring balok.

foto: Istimewa

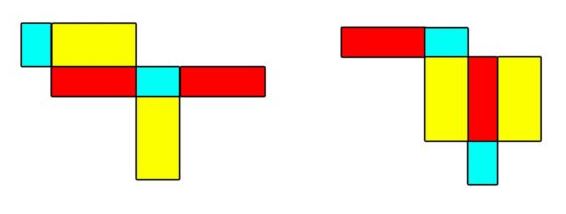
Jaring-jaring balok adalah istilah yang merujuk pada pola atau susunan dari garis-garis dan titik-titik yang membentuk permukaan tiga dimensi yang menyerupai balok atau kubus. Jaring-jaring balok digunakan dalam matematika dan geometri untuk memvisualisasikan atau merepresentasikan bangun ruang tiga dimensi seperti balok, kubus, prisma, dan bentuk-bentuk tiga dimensi lainnya.

Jaring-jaring balok terdiri dari sejumlah garis-garis yang membentuk sisi-sisi dari bangun ruang tersebut. Jika jaring-jaring tersebut dipotong dan dilipat, maka akan membentuk balok sesungguhnya. Jaring-jaring balok adalah alat yang berguna dalam menghitung luas permukaan dan volume bangun ruang tiga dimensi.

Misalnya, jika kamu memiliki sebuah balok dengan panjang, lebar, dan tinggi tertentu. Nah, kamu dapat membuat jaring-jaring balok dengan membagi permukaan luar balok tersebut menjadi sejumlah sisi-sisi yang saling terhubung. Setelah itu, kamu bisa menghitung luas jaring-jaring balok dengan lebih mudah.

Rumus luas jaring-jaring balok.

L = 2 x (pl + pt + lt)

Keterangan:
L = luas jaring-jaring balok
p = panjang balok
l = lebar balok
t = tinggi balok

Ciri-ciri jaring-jaring balok.

foto: Istimewa

1. Jaring-jaring balok terdiri dari enam sisi yang berbentuk persegi panjang.

2. Jaring-jaring balok memiliki tiga pasang sisi yang berhadapan yang sama bentuk dan ukurannya.

3. Jaring-jaring balok memiliki dua belas rusuk yang sejajar berpasangan dan memiliki panjang yang sama.

4. Jaring-jaring balok memiliki delapan titik sudut yang terbentuk dari perpotongan tiga rusuk.

5. Jaring-jaring balok memiliki empat diagonal bidang yang terbentuk dari ruas garis yang menghubungkan dua titik sudut yang saling berhadapan pada satu sisi.

6. Jaring-jaring balok memiliki empat bidang diagonal yang terbentuk dari empat sisi yang saling berpotongan.

Contoh soal luas jaring-jaring balok.

foto: Istimewa

1. Sebuah balok memiliki panjang 15 cm, lebar 10 cm, dan tinggi 8 cm. Berapakah luas jaring-jaring balok tersebut?

Jawaban:

L = 2 x (15 x 10 + 15 x 8 + 10 x 8)
L = 2 x (150 + 120 + 80)
L = 2 x 350
L = 700 cm²

2. Sebuah balok memiliki luas jaring-jaring 440 cm². Jika panjang balok adalah 11 cm dan lebar balok adalah 8 cm, berapakah tinggi balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
440 = 2 x (11 x 8 + 11t + 8t)
440 = 2 x (88 + 19t)
440 = 176 + 38t
264 = 38t
t = 264 / 38
t = 7 cm

3. Sebuah balok memiliki luas jaring-jaring 540 cm². Jika panjang balok adalah 12 cm dan tinggi balok adalah 9 cm, berapakah lebar balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
540 = 2 x (12l + 12 x 9 + 9l)
540 = 2 x (21l + 108)
540 = 42l + 216
324 = 42l
l = 324 / 42
l = 7,71 cm

4. Sebuah balok memiliki luas jaring-jaring 600 cm². Jika lebar balok adalah 10 cm dan tinggi balok adalah 6 cm, berapakah panjang balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
600 = 2 x (10p + 10 x 6 + 6p)
600 = 2 x (16p + 60)
600 = 32p + 120
480 = 32p
p = 480 / 32
p = 15 cm

5. Sebuah balok memiliki luas jaring-jaring 720 cm². Jika panjang, lebar, dan tinggi balok berbanding 3 : 2 : 1, berapakah ukuran sisi-sisi balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
720 = 2 x (3x x 2x + 3x x x + 2x x x)
720 = 2 x (6x² + 3x²2 + 2x²)
720 = 2 x 11x²
720 = 22x²
x^2 = 720 / 22
x^2 = 32,73
x = akar 32,73
x = 5,72 cm

Panjang balok = 3x = 3 x 5,72 = 17,16 cm

Lebar balok = 2x = 2 x 5,72 = 11,44 cm

Tinggi balok = x = 5,72 cm

6. Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 3 cm. Berapakah luas jaring-jaring balok tersebut?

Jawaban:

L = 2 x (8 x 5 + 8 x 3 + 5 x 3)
L = 2 x (40 + 24 + 15)
L = 2 x 79
L = 158 cm²

7. Sebuah balok memiliki luas jaring-jaring 300 cm². Jika panjang balok adalah 10 cm dan lebar balok adalah 5 cm, berapakah tinggi balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
300 = 2 x (10 x 5 + 10t + 5t)
300 = 2 x (50 + 15t)
300 = 100 + 30t
200 = 30t
t = 200 / 30
t = 6,67 cm

8. Sebuah balok memiliki luas jaring-jaring 360 cm². Jika panjang balok adalah 9 cm dan tinggi balok adalah 4 cm, berapakah lebar balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
360 = 2 x (9l + 9 x 4 + 4l)
360 = 2 x (13l + 36)
360 = 26l + 72
288 = 26l
l = 288 / 26
l = 11,08 cm

9. Sebuah balok memiliki luas jaring-jaring 400 cm². Jika lebar balok adalah 8 cm dan tinggi balok adalah 5 cm, berapakah panjang balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
400 = 2 x (8p + 8 x 5 + 5p)
400 = 2 x (13p + 40)
400 = 26p + 80
320 = 26p
p = 320 / 26
p = 12,31 cm

10. Sebuah balok memiliki luas jaring-jaring 480 cm². Jika panjang, lebar, dan tinggi balok berbanding 4 : 3 : 2, berapakah ukuran sisi-sisi balok tersebut?

Jawaban:

L = 2 x (pl + pt + lt)
480 = 2 x (4x x 3x + 4x x 2x + 3x x 2x)
480 = 2 x (12x² + 8x² + 6x²)
480 = 2 x 26x²
480 = 52x²
x² = 480 / 52
x² = 9,23
x = akar 9,23
x = 3,04 cm

Panjang balok = 4x = 4 x 3,04 = 12,16 cm

Lebar balok = 3x = 3 x 3,04 = 9,12 cm

Tinggi balok = 2x = 2 x 3,04 = 6,08 cm

11. Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 4 cm. Berapakah luas jaring-jaring balok tersebut?

Jawaban:

L = 2 x (10 x 6 + 10 x 4 + 6 x 4)
L = 2 x (60 + 40 + 24)
L = 2 x 124
L = 248 cm²