Rumus luas layang-layang, lengkap dengan contoh soal dan pembahasannya

Brilio.net - Sadar nggak sih, kalau hampir semua benda yang ada di sekitar kita itu bisa dihitung luasnya, termasuk layang-layang. Kamu pasti sering menemui soal-soal tentang layang-layang yang kerap muncul dalam ujian sekolah maupun ujian nasional. Nggak cuma itu, dalam pelajaran matematika sehari-hari, guru juga sering mencontohkan bagaimana menghitung luas layang-layang.

Oleh sebab itu, penting banget untuk pelajari materi tentang layang-layang ini. Layang-layang merupakan bangun datar yang berbentuk segiempat dan memiliki dua pasang sisi dan sama panjang. Selain itu, persegi panjang dalam layang-layang juga memiliki bentuk seperti belah ketupat namun tidak memiliki keempat sisi yang sama.

Nah, supaya kamu nggak bingung lagi tentang materi layang-layang, berikut dijelaskan rumus luas layang-layang yang lengkap dengan contoh soal dan pembahasannya, dilansir brilio.net dari berbagai sumber pada Senin (4/9).

Pengertian layang-layang

foto: Istimewa

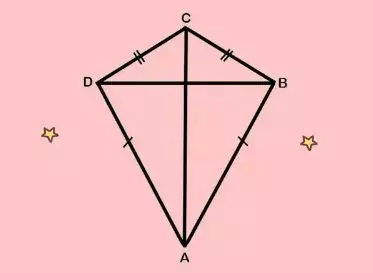
Layang-layang adalah suatu bentuk geometri dua dimensi yang terdiri dari dua pasang sisi yang memiliki panjang berbeda. Sedangkan keempat sisinya membentuk sudut-sudut yang tidak sama besar. Dalam layang-layang, dua pasang sisi berhadapan satu sama lain dan biasanya memiliki panjang yang sama, sedangkan panjang dua pasang sisi lainnya berbeda.

Adapun ciri-ciri utama dari layang-layang adalah:

1. Mempunyai empat sisi.

Layang-layang memiliki empat sisi. Dua sisi yang berhadapan satu sama lain biasanya memiliki panjang yang sama, dan dua sisi lainnya berbeda panjang.

2. Empat sudut.

Layang-layang memiliki empat sudut. Sudut-sudut ini mungkin tidak sama besar, tergantung pada panjang sisi-sisinya.

3. Dua diagonal.

Layang-layang memiliki dua diagonal yang menghubungkan sudut-sudut yang berlawanan. Diagonal ini biasanya memiliki panjang yang berbeda.

Layang-layang tidak selalu berbentuk sama, karena panjang sisi-sisinya dapat berbeda-beda, sehingga sudut-sudutnya pun bisa bervariasi. Meskipun demikian, dalam layang-layang yang paling umum, dua pasang sisi yang berhadapan membentuk sudut siku-siku, dan sisanya membentuk sudut yang tidak siku.

 

 

Pengertian luas layang-layang dan rumusnya

foto: Istimewa

Luas layang-layang adalah ukuran total dari area atau bidang yang terdapat di dalam bentuk geometri dua dimensi yang disebut layang-layang. Untuk menghitung luas layang-layang, kamu bisa menggunakan rumus khusus yang bergantung pada panjang kedua diagonalnya dan sudut di antara keduanya.

Rumus umum untuk menghitung luas layang-layang adalah sebagai berikut:

foto: Istimewa

Luas Layang-Layang = (Diagonal 1 x Diagonal 2) / 2 x sin(θ)

Dalam rumus ini:

- "Diagonal 1" dan "Diagonal 2" adalah panjang kedua diagonal layang-layang yang berpotongan di tengah.

- "θ" adalah besar sudut antara kedua diagonal tersebut (dalam radian).

Contoh soal rumus luas layang-layang dan pembahasannya

foto: freepik.com

Soal 1.

Sebuah layang-layang memiliki dua diagonal dengan panjang 8 cm dan 10 cm. Sudut antara kedua diagonalnya adalah 60 derajat. Hitunglah luas layang-layang tersebut.

Penyelesaian 1:

Diagonal 1 (d1) = 8 cm

Diagonal 2 (d2) = 10 cm

Sudut (θ) = 60 derajat = (60 x π) / 180 radian = π/3 radian

Luas Layang-Layang = (d1 x d2) / 2 x sin(θ)

Luas Layang-Layang = (8 cm x 10 cm) / 2 x sin(π/3)

Luas Layang-Layang = (80 cm²) / 2 x (√3/2)

Luas Layang-Layang = 40 cm² x (√3/2)

Jadi, luas layang-layang tersebut adalah 40√3 cm².

Soal 2.

Sebuah layang-layang memiliki dua diagonal dengan panjang 12 cm dan 16 cm. Sudut antara kedua diagonalnya adalah 120 derajat. Hitunglah luas layang-layang tersebut.

Penyelesaian 2:

Diagonal 1 (d1) = 12 cm

Diagonal 2 (d2) = 16 cm

Sudut (θ) = 120 derajat = (120 x π) / 180 radian = 2π/3 radian

Luas Layang-Layang = (d1 x d2) / 2 x sin(θ)

Luas Layang-Layang = (12 cm x 16 cm) / 2 x sin(2π/3)

Luas Layang-Layang = (192 cm²) / 2 x (-√3/2)

Luas Layang-Layang = -96 cm^2 x (√3/2)

Karena luas tidak bisa negatif, maka kita ambil nilai positifnya:

Luas Layang-Layang = 96 cm² x (√3/2)

Jadi, luas layang-layang tersebut adalah 48√3 cm².

Soal 3.

Sebuah layang-layang memiliki diagonal 1 sepanjang 10 cm dan diagonal 2 sepanjang 14 cm. Sudut antara kedua diagonalnya adalah 45 derajat. Hitunglah luas layang-layang tersebut.

Penyelesaian 3:

Diagonal 1 (d1) = 10 cm

Diagonal 2 (d2) = 14 cm

Sudut (θ) = 45 derajat = (45 x π) / 180 radian = π/4 radian

Luas Layang-Layang = (d1 x d2) / 2 x sin(θ)

Luas Layang-Layang = (10 cm x 14 cm) / 2 x sin(π/4)

Luas Layang-Layang = (140 cm²) / 2 x (√2/2)

Luas Layang-Layang = 70 cm² x (√2/2)

Jadi, luas layang-layang tersebut adalah 35√2 cm².

Soal 4.

Sebuah layang-layang memiliki diagonal 1 sepanjang 6 cm dan diagonal 2 sepanjang 8 cm. Sudut antara kedua diagonalnya adalah 150 derajat. Hitunglah luas layang-layang tersebut.

Penyelesaian 4:

Diagonal 1 (d1) = 6 cm

Diagonal 2 (d2) = 8 cm

Sudut (θ) = 150 derajat = (150 x π) / 180 radian = 5π/6 radian

Luas Layang-Layang = (d1 x d2) / 2 x sin(θ)

Luas Layang-Layang = (6 cm x 8 cm) / 2 x sin(5π/6)

Luas Layang-Layang = (48 cm^2) / 2 x (-1/2)

Luas Layang-Layang = -24 cm²

Karena luas tidak bisa negatif, maka kita ambil nilai positifnya:

Luas Layang-Layang = 24 cm²

Jadi, luas layang-layang tersebut adalah 24 cm².

Soal 5.

Sebuah layang-layang memiliki diagonal 1 sepanjang 9 cm dan diagonal 2 sepanjang 12 cm. Sudut antara kedua diagonalnya adalah 90 derajat. Hitunglah luas layang-layang tersebut.

Penyelesaian 5:

Diagonal 1 (d1) = 9 cm

Diagonal 2 (d2) = 12 cm

Sudut (θ) = 90 derajat = (90 x π) / 180 radian = π/2 radian

Luas Layang-Layang = (d1 x d2) / 2 x sin(θ)

Luas Layang-Layang = (9 cm x 12 cm) / 2 x sin(π/2)

Luas Layang-Layang = (108 cm²) / 2 x 1

Luas Layang-Layang = 108 cm²

Jadi, luas layang-layang tersebut adalah 108 cm².