Rumus luas permukaan balok, lengkap dengan contoh soal dan penyelesaiannya

Brilio.net - Materi matematika yang kerap ditemukan adalah tentang luas permukaan balok. Ruang tiga dimensi yang kerap ditemukan dalam kehidupan sehari-hari ini memiliki panjang, tinggi, dan volume.

Nah, dalam memahami rumus luas permukaan balok ternyata tidak terlalu sulit. Kamu hanya perlu memahami tentang konsep dasar balok yang memiliki rumus paten untuk mencari luas permukaan balok itu sendiri. Selain itu, penting dipahami bahwa permukaan balok memiliki sifat dan bentuk yang khas, yaitu 6 sisi berbentuk persegi panjang, 12 rusuk dengan panjang yang berbeda, dan 12 diagonal bidang.

Balok juga memiliki 4 diagonal ruang dan 6 bidang diagonal persegi panjang. Nah dari setiap sisi, bentuk, dan diagonal ini akan menghasilkan rumus luas permukaan balok yang paten. Langsung saja, berikut rumus luas permukaan balok, lengkap dengan contoh soal dan penyelesaiannya yang dilansir brilio.net dari berbagai sumber, Rabu (30/8).

Rumus luas permukaan balok.

foto: Istimewa

Rumus luas permukaan balok adalah suatu formula matematis yang digunakan untuk menghitung luas total dari semua sisi yang membentuk permukaan luar balok. Merujuk buku pelajaran Kapita Selekta Matematika SMP, luas permukaan balok merupakan total luas seluruh sisi pada sebuah balok. Oleh karena itu, penting untuk mengetahui bentuk dan ukuran setiap sisinya.

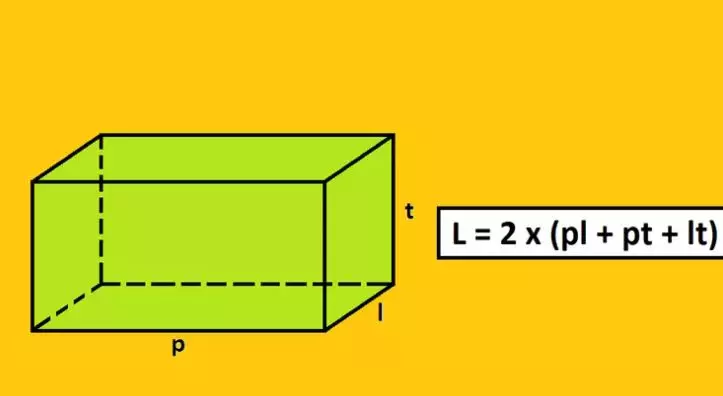
Bentuk balok.

foto: Istimewa

Balok memiliki bangun ruang tiga pasang sisi yang saling berhadapan. Bentuk dan ukuran balok ini memiliki sisi dan bentuk persegi panjang yang sama. Apabila dijumlahkan, terdapat 6 sisi yang menyusun balok sehingga luas permukaan balok dengan jumlah ketiga sisi tersebut dikalikan dua.

Sehingga balok memiliki 12 rusuk yang dapat dikelompokkan menjadi:

1. Rusuk panjang (p) : AB, CD, EF, GH

2. Rusuk lebar (l) : AD, BC, EH, FG

3. Rusuk tinggi (t) : AE, DH, BF, CG

Luas sisi alas = atas = p x lebar

Luas sisi kanan = kiri = l x t

Luas sisi depan = belakang = p x t

Secara umum, rumus untuk menghitung luas permukaan balok (L) adalah sebagai berikut:

Luas Permukaan Balok = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)

L = 2 x [(p x l)+(p x t)+(l x t)]

Rumus alternatif permukaan dari luas balok:

L = 2pl + 2lt + 2pt
V = p x l x t
P = V : (l x t)

Rumus luas permukaan balok tanpa tutup:

L = pl + 2(lt) + 2(pt)

Dimana:
L = luas permukaan

p = panjang

l = lebar

t = tinggi

Contoh soal luas permukaan balok dan penyelesaiannya.

foto: pexels.com

Contoh soal 1.

Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 3 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas permukaan balok dapat dihitung dengan rumus:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (8 cm × 5 cm + 8 cm × 3 cm + 5 cm × 3 cm) = 2 × (40 cm² + 24 cm² + 15 cm²) = 2 × 79 cm² = 158 cm².

Contoh soal 2.

Sebuah balok memiliki panjang 12 cm, lebar 6 cm, dan tinggi 4 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (12 cm × 6 cm + 12 cm × 4 cm + 6 cm × 4 cm) = 2 × (72 cm² + 48 cm² + 24 cm²) = 2 × 144 cm² = 288 cm².

Contoh soal 3.

Sebuah balok memiliki panjang 10 cm, lebar 8 cm, dan tinggi 5 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (10 cm × 8 cm + 10 cm × 5 cm + 8 cm × 5 cm) = 2 × (80 cm² + 50 cm² + 40 cm²) = 2 × 170 cm² = 340 cm².

Contoh soal 4.

Sebuah balok memiliki panjang 15 cm, lebar 7 cm, dan tinggi 6 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (15 cm × 7 cm + 15 cm × 6 cm + 7 cm × 6 cm) = 2 × (105 cm² + 90 cm² + 42 cm²) = 2 × 237 cm² = 474 cm².

Contoh soal 5.

Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 10 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (6 cm × 4 cm + 6 cm × 10 cm + 4 cm × 10 cm) = 2 × (24 cm² + 60 cm² + 40 cm²) = 2 × 124 cm² = 248 cm².

foto: pexels.com

Contoh soal 6.

Sebuah balok memiliki panjang 9 cm, lebar 3 cm, dan tinggi 8 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (9 cm × 3 cm + 9 cm × 8 cm + 3 cm × 8 cm) = 2 × (27 cm² + 72 cm² + 24 cm²) = 2 × 123 cm² = 246 cm².

Contoh soal 7.

Sebuah balok memiliki panjang 20 cm, lebar 10 cm, dan tinggi 15 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (20 cm × 10 cm + 20 cm × 15 cm + 10 cm × 15 cm) = 2 × (200 cm² + 300 cm² + 150 cm²) = 2 × 650 cm² = 1300 cm².

Contoh soal 8.

Sebuah balok memiliki panjang 25 cm, lebar 6 cm, dan tinggi 12 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (25 cm × 6 cm + 25 cm × 12 cm + 6 cm × 12 cm) = 2 × (150 cm² + 300 cm² + 72 cm²) = 2 × 522 cm² = 1044 cm².

Contoh soal 9.

Sebuah balok memiliki panjang 18 cm, lebar 9 cm, dan tinggi 7 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (18 cm × 9 cm + 18 cm × 7 cm + 9 cm × 7 cm) = 2 × (162 cm² + 126 cm² + 63 cm²) = 2 × 351 cm² = 702 cm².

Contoh soal 10.

Sebuah balok memiliki panjang 30 cm, lebar 12 cm, dan tinggi 9 cm. Hitunglah luas permukaan balok ini.

Jawaban:

Luas = 2 × (panjang × lebar + panjang × tinggi + lebar × tinggi).

Luas = 2 × (30 cm × 12 cm + 30 cm × 9 cm + 12 cm × 9 cm) = 2 × (360 cm² + 270 cm² + 108 cm²) = 2 × 738 cm^2 = 1476 cm².