Rumus luas permukaan bandul, lengkap dengan ciri dan contoh soalnya

Brilio.net - Salah satu topik yang sering dipelajari dalam matematika adalah permukaan bandul. Permukaan bandul adalah ukuran luas dari semua sisi yang membentuk bandul. Nah, kamu pasti nggak asing lagi dengan bentuk bandul.

Bandul adalah benda yang terdiri dari dua atau lebih bentuk geometri yang disatukan, seperti setengah bola dan kerucut, atau bola dan kubus, atau limas dan setengah bola, atau prisma dan setengah bola.

Untuk mencari permukaan bandul, kamu harus mengetahui rumus permukaan dari masing-masing bentuk geometri yang menyusun bandul, kemudian menjumlahkan permukaan dari semua sisi yang terlihat.

Dalam artikel ini, brilio.net akan membahas tentang materi matematika yang membahas tentang luas permukaan bandul, mulai dari pengertian, rumus, contoh soal, hingga pembahasannya. Yuk simak selengkapnya yang telah dirangkum dari berbagai sumber pada Jumat (12/10).

Pengertian permukaan bandul.

foto: Istimewa

Permukaan bandul mengacu pada bagian luar atau lapisan luar dari sebuah bandul fisik. Bandul adalah benda yang digantung di suatu titik, biasanya dari sebuah tali atau batang, dan bisa bergerak bebas di sekitar titik gantungan. Permukaan bandul adalah bagian luar yang mencakup semua area di sekitar bandul tersebut. Permukaan bandul ini akan berbeda tergantung pada bentuk, ukuran, dan bahan dari bandul itu sendiri.

Bandul dapat memiliki berbagai bentuk dan ukuran. Ini bisa berupa bola, cakram, silinder, atau bentuk lainnya. Permukaan bandul seringkali merupakan benda tiga dimensi dengan bentuk yang khusus, dan bagian ini mencakup area luar dari bandul yang mungkin berinteraksi dengan lingkungannya.

Misalnya, jika bandul adalah bola yang digantung dari seutas tali, permukaan bandul akan menjadi bagian luar dari bola tersebut, yang mencakup seluruh permukaan bola. Permukaan bandul ini adalah bagian yang akan terpapar pada lingkungan sekitarnya dan dapat mempengaruhi pergerakan bandul, misalnya jika ada gesekan antara permukaan bandul dan udara atau permukaan yang bersentuhan dengannya.

Jadi, permukaan bandul adalah bagian luar dari bandul yang mencakup seluruh area luar atau bagian luar yang dapat berinteraksi dengan lingkungannya.

 

Pengertian dan ciri luas permukaan bandul.

foto: Istimewa

Luas permukaan bandul adalah ukuran luas dari semua sisi yang membentuk bandul. Bandul adalah benda yang terdiri dari dua atau lebih bentuk geometri yang disatukan. Biasanya, bandul terdiri dari setengah bola dan kerucut, atau bola dan kubus, atau limas dan setengah bola, atau prisma dan setengah bola.

Untuk mencari luas permukaan bandul, kamu harus mengetahui rumus luas permukaan dari masing-masing bentuk geometri yang menyusun bandul, kemudian menjumlahkan luas permukaan dari semua sisi yang terlihat. Berikut adalah beberapa ciri-ciri luas permukaan bandul:

1. Luas permukaan bandul selalu lebih besar dari luas permukaan salah satu bentuk geometri yang menyusunnya.

2. Luas permukaan bandul bergantung pada ukuran dan bentuk dari masing-masing bentuk geometri yang menyusunnya.

3. Luas permukaan bandul berubah jika ada perubahan pada ukuran atau bentuk dari salah satu bentuk geometri yang menyusunnya.

4. Luas permukaan bandul dapat dihitung dengan menggunakan rumus matematika atau dengan menggunakan alat ukur seperti jangka sorong atau meteran.

5. Luas permukaan bandul biasanya diukur dalam satuan luas, seperti cm², m², atau km².

Rumus luas permukaan bandul.

foto: freepik.com

Rumus untuk menghitung luas permukaan bandul (pendulum) adalah sebagai berikut:

Luas Permukaan Bandul = 2πr² + (2/3)πr³

Dalam rumus ini:

- "r" adalah panjang tali (radius) dari bandul, yaitu jarak antara pusat massa bandul ke titik tali yang digantungkan.

- π (Pi) adalah konstanta matematika yang sekitar 3.14159.

Rumus ini digunakan untuk menghitung luas permukaan bandul fisik dengan bentuk tertentu yang memiliki massa yang didistribusikan merata dalam bentuk lingkaran atau bola di ujung tali. Rumus ini menggabungkan luas permukaan bola dengan luas permukaan lingkaran yang merupakan bentuk umum dari bandul yang diukur dalam teori fisika. Luas permukaan bandul bisa bergantung pada bentuk atau konfigurasi spesifik bandul tersebut.

Contoh soal luas permukaan bandul dan penyelesaiannya.

foto: Istimewa

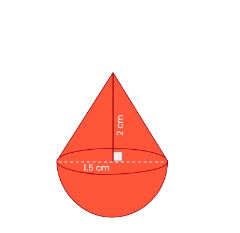
1. Sebuah bandul terdiri dari setengah bola dengan jari-jari 5 cm dan kerucut dengan jari-jari 5 cm dan tinggi 10 cm. Berapakah luas permukaan bandul tersebut?

Jawaban:
Luas permukaan bandul = luas selimut setengah bola + luas selimut kerucut

Luas selimut setengah bola = 2πr²

Luas selimut kerucut = πrl, dengan l adalah panjang garis pelukis kerucut

Untuk mencari l, kamu dapat menggunakan teorema Pythagoras:

l² = r² + t², dengan t adalah tinggi kerucut

l = √(r²2 + t²)

l = √(5² + 10²)

l = √(25 + 100)

l = √125

l ≈ 11,18 cm

Maka, luas permukaan bandul = 2π(5)² + π(5)(11,18)

Luas permukaan bandul ≈ 314,16 + 176,71

Luas permukaan bandul ≈ 490,87 cm²

2. Sebuah bandul terbuat dari kubus dengan panjang sisi 8 cm dan bola dengan jari-jari 4 cm. Bola ditempelkan pada salah satu sisi kubus. Berapakah luas permukaan bandul tersebut?

Jawaban:
Luas permukaan bandul = luas permukaan kubus - luas sisi kubus yang ditempel bola + luas permukaan bola

Luas permukaan kubus = 6s², dengan s adalah panjang sisi kubus
Luas sisi kubus yang ditempel bola = s²

Luas permukaan bola = 4πr², dengan r adalah jari-jari bola

Maka, luas permukaan bandul = 6(8)² - (8)² + 4π(4)²

Luas permukaan bandul = 288 - 64 + 201,06

Luas permukaan bandul ≈ 425,06 cm²

3. Sebuah bandul terbuat dari limas segiempat dengan panjang sisi alas 6 cm dan tinggi tegaknya 8 cm. Di atas limas terdapat setengah bola dengan jari-jari sama dengan setengah panjang sisi alas limas. Berapakah luas permukaan bandul tersebut?

Jawaban:
Luas permukaan bandul = luas alas limas + luas selimut limas + luas selimut setengah bola

Luas alas limas = s² dengan s adalah panjang sisi alas limas

Luas selimut limas = 4 × (1/2) × s × t, dengan t adalah tinggi segitiga siku-siku yang merupakan sisi miring limas

Untuk mencari t, kita dapat menggunakan teorema Pythagoras:

t² = (s/2)² + h², dengan h adalah tinggi tegak limas

t = √((s/2)² + h²)

t = √((6/2)² + 8²)

t = √(9 + 64)

t = √73

t ≈ 8,54 cm

Luas selimut setengah bola = 2πr², dengan r adalah jari-jari setengah bola

r = s/2

r = 6/2

r = 3 cm

Maka, luas permukaan bandul = (6)² + 4 × (1/2) × (6) × (8,54) + 2π(3)²

Luas permukaan bandul = 36 + 102,96 + 56,55

Luas permukaan bandul ≈ 195,51 cm²

4. Sebuah bandul terbuat dari prisma segitiga sama kaki dengan panjang sisi alas 12 cm dan tinggi 15 cm. Prisma memiliki tinggi 20 cm. Di atas prisma terdapat setengah bola dengan jari-jari sama dengan setengah panjang sisi alas prisma. Berapakah luas permukaan bandul tersebut?

Jawaban:
Luas permukaan bandul = luas alas prisma + luas selimut prisma + luas selimut setengah bola

Luas alas prisma = (1/2) × a × t, dengan a adalah panjang sisi alas prisma dan t adalah tinggi segitiga alas prisma

Luas selimut prisma = keliling alas prisma × tinggi prisma

Keliling alas prisma = 3a, karena segitiga sama kaki memiliki tiga sisi yang sama panjang

Luas selimut setengah bola = 2πr², dengan r adalah jari-jari setengah bola

r = a/2

r = 12/2

r = 6 cm

Maka, luas permukaan bandul = (1/2) × (12) × (15) + 3(12) × (20) + 2π(6)²

Luas permukaan bandul = 90 + 720 + 226,19

Luas permukaan bandul ≈ 1036,19 cm²

5. Sebuah bandul terbuat dari bola dengan jari-jari 10 cm yang dipotong menjadi dua bagian yang tidak sama besar. Bagian yang lebih besar memiliki tinggi 12 cm. Bagian yang lebih kecil ditempelkan pada bagian yang lebih besar sehingga membentuk bandul. Berapakah luas permukaan bandul tersebut?

Jawaban:
Luas permukaan bandul = luas selimut bagian bola yang lebih besar + luas selimut bagian bola yang lebih kecil - luas lingkaran yang menjadi tempat potongan

Luas selimut bagian bola yang lebih besar = 2πrh, dengan r adalah jari-jari bola dan h adalah tinggi bagian bola yang lebih besar

Luas selimut bagian bola yang lebih kecil = 2πrh, dengan r adalah jari-jari bola dan h adalah tinggi bagian bola yang lebih kecil

Untuk mencari h, gunakan rumus berikut:

h = r - √(r² - d²), dengan d adalah jari-jari lingkaran yang menjadi tempat potongan

d = r - h

d = 10 - 12

d = -2 cm

Karena d tidak mungkin bernilai negatif, maka kita harus mengambil nilai mutlaknya.

d = | -2 |

d = 2 cm

h = r - √(r² - d²)

h = 10 - √(10² - 2²)

h = 10 - √(100 - 4)

h = 10 - √96

h ≈ 10 - 9,80

h ≈ 0,20 cm

Luas lingkaran yang menjadi tempat potongan = πd², dengan d adalah jari-jari lingkaran tersebut

Maka, luas permukaan bandul = 2π(10)(12) + 2π(10)(0,20) - π(2)²

Luas permukaan bandul ≈ 753,98 + 12,57 - 12,57

Luas permukaan bandul ≈ 753,98 cm²