Rumus luas segitiga sama sisi beserta karakteristik, contoh soal, dan cara pengerjaannya

Brilio.net - Segitiga merupakan salah satu bangun datar yang memiliki tiga sisi yang saling berpotongan dan menciptakan tiga titik sudut. Segitiga juga dapat dibedakan menjadi dua jenis, yaitu segitiga berdasarkan panjang sisinya dan segitiga berdasarkan sudutnya.

Nggak hanya dalam ilmu matematika, bangun datar segitiga sama sisi juga dapat ditemukan dalam kehidupan sehari-hari, misalnya bagian atap rumah. Jika dilihat dari jauh, atap rumah membentuk segitiga sama sisi.

Nah, supaya lebih memahami tentang segitiga sama sisi, kali ini brilio.net akan membahas tentang rumus luas segitiga sama sisi lengkap dengan karakteristik, contoh soal, dan cara pengerjaannya yang dihimpun dari berbagai sumber pada Rabu (18/10).

Pengertian dan rumus luas segitiga sama sisi.

Rumus luas segitiga sama sisi
Istimewa

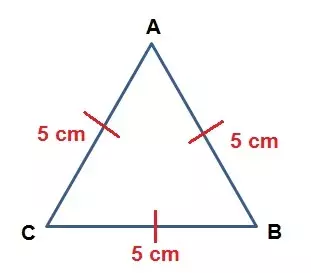
Segitiga sama sisi adalah segitiga yang memiliki tiga sisi dengan panjang yang sama. Ketiga sudut segitiga sama sisi juga memiliki ukuran yang sama, yaitu 60 derajat. Segitiga ini memiliki sifat khusus dan merupakan salah satu jenis segitiga yang dikenal dalam geometri.

Ciri-ciri segitiga sama sisi:

1. Semua sisinya memiliki panjang yang sama
2. Ketiga sudutnya memiliki ukuran yang sama, yaitu 60 derajat
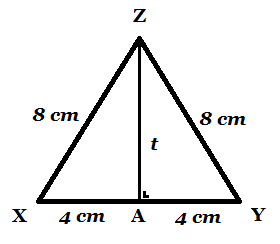
3. Garis tinggi (garis yang ditarik dari salah satu sudut segitiga ke sisi yang berlawanan) juga sama panjangnya dan membentuk garis tinggi yang sama.

Segitiga sama sisi memiliki keunikan dalam hal sifat-sifatnya dan seringkali digunakan dalam berbagai konsep dan perhitungan geometri. Rumus luas segitiga sama sisi adalah sebagai berikut.

Luas = (s^2 * √3)/4

Rumus ini memanfaatkan panjang sisi (s) untuk menghitung luas segitiga. Simbol √3 melambangkan akar kuadrat dari 3 (sekitar 1,732). Rumus ini juga mengalikan panjang sisi dengan dirinya sendiri (s^2) dengan dengan √3 dan kemudian dibagi 4.

Karakteristik segitiga sama sisi.

Rumus luas segitiga sama sisi
Istimewa

Segitiga sama sisi memiliki karakteristik khusus yang membedakannya dari segitiga lainnya. Berikut adalah beberapa karakteristik utama segitiga sama sisi:

1. Sisi-sisi dengan panjang yang sama.

Segitiga sama sisi memiliki tiga sisi yang memiliki panjang yang sama. Ini berarti semua sisi segitiga memiliki panjang yang identik.

2. Sudut-sudut yang sama.

Segitiga ini memiliki tiga sudut yang sama besar, yaitu 60 derajat. Ketiga sudut ini disebut sudut-sudut sama sisi.

3. Keliling yang sama.

Keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya. Dalam segitiga ini, kelilingnya adalah tiga kali panjang sisi, karena semua sisinya sama panjang.

4. Garis Tinggi yang sama.

Segitiga sama sisi memiliki garis tinggi yang memiliki panjang yang sama dari setiap sudut ke sisi yang berlawanan.

5. Simetri.

Segitiga ini memiliki banyak simetri. Jika kamu menggambar garis dari sudut ke sudut yang berlawanan, segitiga akan tampak sama dari kedua sisi garis ini. Ini disebut simetri pusat.

6. Luas yang Tertentu.

Luas segitiga sama sisi dapat dihitung dengan menggunakan rumus khusus, yaitu (s^2 * √3)/4, di mana "s" adalah panjang sisi.

7. Konstruksi Sederhana.

Segitiga sama sisi dapat dengan mudah dibangun dengan menggunakan kompas dan penggaris, karena semua sisinya sama panjang.

Contoh soal dan cara pengerjaannya.

Rumus luas segitiga sama sisi
Istimewa

1. Sebuah segitiga sama sisi memiliki panjang sisi 6 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 6 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (6^2 * √3)/4
Luas = (36 * √3)/4
Luas = (9√3) cm²

Jadi, luas segitiga sama sisi adalah 9√3 cm².

2. Sebuah segitiga sama sisi memiliki panjang sisi 8 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 8 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (8^2 * √3)/4
Luas = (64 * √3)/4
Luas = (16√3) cm²

Jadi, luas segitiga sama sisi adalah 16√3 cm².

3 Sebuah segitiga sama sisi memiliki panjang sisi 12 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 12 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (12^2 * √3)/4
Luas = (144 * √3)/4
Luas = (36√3) cm²

Jadi, luas segitiga sama sisi adalah 36√3 cm².

4. Sebuah segitiga sama sisi memiliki panjang sisi 10 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 10 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (10^2 * √3)/4
Luas = (100 * √3/4
Luas = (25√3) cm²

Jadi, luas segitiga sama sisi adalah 25√3 cm².

5. Sebuah segitiga sama sisi memiliki panjang sisi 5 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 5 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (5^2 * √3/4
Luas = (25 * √3)/4
Luas = (6.25√3) cm²

Jadi, luas segitiga sama sisi adalah 6.25√3 cm².

6. Sebuah segitiga sama sisi memiliki panjang sisi 15 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 15 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (15^2 * √3)/4
Luas = (225 * √3)/4
Luas = (56.25√3) cm²

Jadi, luas segitiga sama sisi adalah 56.25√3 cm².

7. Sebuah segitiga sama sisi memiliki panjang sisi 7 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 7 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (7^2 * √3)/4
Luas = (49 * √3)/4
Luas = (12.25√3) cm²

Jadi, luas segitiga sama sisi adalah 12.25√3 cm².

8. Sebuah segitiga sama sisi memiliki panjang sisi 9 cm. Hitunglah luas segitiga tersebut.

Pembahasan:

Diketahui panjang sisi = 9 cm, maka dapat dihitung dengan rumus luas segitiga sama sisi

Luas = (s^2 * √3)/4
Luas = (9^2 * √3)/4
Luas = (81 * √3)/4
Luas = (20.25√3) cm²

Jadi, luas segitiga sama sisi adalah 20.25√3 cm².