Rumus luas segitiga siku-siku, beserta ciri, contoh soal dan cara pengerjaannya

Brilio.net - Bagi sebagai pelajar, pelajaran matematika jadi salah satu momok yang menakutkan. Padahal, pelajaran satu ini memiliki materi pembelajaran yang mudah dipahami, lho. Salah satunya seputar segitiga siku-siku yang salah satu sudutnya bernilai 90 derajat. Di mana hubungan antara sisi dan sudut segitiga siku-siku menjadi dasar dari sebuah nilai trigonometri.

Sisi yang berseberangan dengan sudut siku-siku disebut hipotenusa. Sementara itu, sisi-sisi lain yang berdekatan dengan sudut kanan disebut kaki atau katet. Sisi A dapat diidentifikasi sebagai sisi yang berdekatan dengan sudut B dan berlawanan dengan (atau berlawanan) sudut A, sedangkan sisi B adalah sisi yang berdekatan dengan sudut A dan berlawanan dengan sudut B.

Dari sudut dan sisi tersebut membentuk segitiga siku-siku dengan rumus luas, diagonal, dan volumenya tersendiri. Supaya lebih mudah menyelesaikan soal ujian tentang luas segitiga siku-siku ini, berikut brilio.net berikan penjelasan lengkap rumus luas segitiga siku-siku, beserta ciri, contoh soal dan cara pengerjaannya. Dihimpun dari berbagai sumber pada Jumat (15/9).

Ciri-ciri luas segitiga siku-siku

foto: freepik.com

1. Segitiga siku-siku memiliki satu sudut siku-siku (90°) dan dua sudut lancip (di bawah 90°).

2. Segitiga siku-siku memiliki dua sisi yang saling tegak lurus pada sudut siku-siku. Sisi-sisi ini disebut kaki-kaki segitiga.

3. Segitiga siku-siku memiliki satu sisi miring yang berseberangan dengan sudut siku-siku. Sisi ini disebut hipotenusa segitiga. Hipotenusa adalah sisi terpanjang dari segitiga siku-siku.

4. Segitiga siku-siku memiliki satu sumbu simetri pada segitiga siku-siku sama kaki. Sumbu simetri adalah garis yang membagi segitiga menjadi dua bagian yang sama besar dan bentuknya. Pada segitiga siku-siku sama kaki, sumbu simetri melalui sudut siku-siku dan titik tengah hipotenusa.

5. Segitiga siku-siku memiliki hubungan antara sisi dan sudut yang disebut trigonometri. Trigonometri adalah cabang matematika yang mempelajari hubungan antara panjang sisi dan besar sudut pada segitiga, khususnya segitiga siku-siku. Trigonometri menggunakan fungsi-fungsi seperti sinus, kosinus, dan tangen untuk menghitung nilai-nilai tersebut.

Rumus luas segitiga siku-siku

foto: Istimewa

Luas segitiga siku-siku adalah ukuran bidang datar yang dibatasi oleh tiga sisi segitiga yang salah satu sudutnya adalah sudut siku-siku (90°). Luas segitiga siku-siku dapat dihitung dengan rumus:

L = 1/2 × alas × tinggi

Di mana alas dan tinggi adalah panjang sisi-sisi yang saling tegak lurus pada sudut siku-siku. Luas segitiga siku-siku biasanya dinyatakan dalam satuan persegi, misalnya sentimeter persegi (cm²) atau meter persegi (m²).

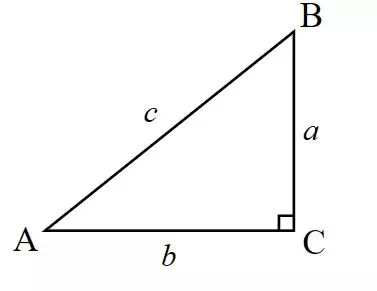
Untuk lebih jelasnya, kamu bisa melihat gambar berikut:

foto: Istimewa

Pada gambar di atas, segitiga ABC adalah segitiga siku-siku di B. Sisi AB dan BC adalah alas dan tinggi segitiga, sedangkan sisi AC adalah hipotenusa (sisi miring). Luas segitiga ABC dapat dihitung dengan rumus:

L = 1/2 × AB × BC

Contoh soal luas segitiga siku-siku

Contoh 1

Sebuah segitiga siku-siku memiliki panjang alas 10cm dan tinggi 8 cm. Hitunglah luas segitiga siku-siku tersebut!

Jawaban:

Luas segitiga siku-siku = 1/2 × alas × tinggi
Luas segitiga siku-siku = 1/2 × 10 cm × 8 cm
Luas segitiga siku-siku = 40 cm²

Contoh 2

Sebuah benda berbentuk segitiga siku-siku memiliki panjang alas 20 cm dan tinggi 40 cm. Berapakan luas benda tersebut?

Jawaban:

Luas benda = luas segitiga siku-siku
Luas benda = 1/2 × alas × tinggi
Luas benda = 1/2 × 20 cm × 40 cm
Luas benda = 400 cm²

Contoh 3

Sebuah segitiga siku-siku memiliki sisi miring 13 cm dan tinggi 5 cm. Berapakah luas segitiga siku-siku tersebut?

Jawaban:

Untuk mencari luas segitiga siku-siku, perlu mengetahui panjang alasnya. Kamu bisa menggunakan rumus Phytagoras untuk mencari alas, yaitu c² = a² + b², di mana c adalah hipotenusa (sisi miring), a adalah alas, dan b adalah tinggi.

c² = a² + b²
(13 cm)² = a² + (5 cm)²
169 cm² = a² + 25 cm²
a2 = 169 cm² - 25 cm²
a2 = 144 cm²
a = akar pangkat dua dari 144 cm²
a = 12 cm

Jadi, panjang alas segitiga siku-siku adalah 12 cm. Selanjutnya, bisa mencari luas segitiga siku-siku dengan rumus:

Luas segitiga siku-siku = 1/2 × alas × tinggi
Luas segitiga siku-siku = 1/2 × 12 cm × 5 cm
Luas segitiga siku-siku = 30 cm²

Contoh 4

Sebuah layang-layang berbentuk segitiga. Jika panjang AB adalah 24 cm dan panjang BC adalah 18 cm, berapakah luas layang-layang tersebut?

Jawaban:

Untuk mencari luas layang-layang, kita bisa membagi layang-layang menjadi dua buah segitiga siku-siku yang sama besar dan bentuknya, yaitu segitiga ABC dan segitiga ACD. Kita bisa mencari luas salah satu segitiga siku-siku dengan rumus:

Luas segitiga siku-siku = 1/2 × alas × tinggi
Luas segitiga ABC = 1/2 × AB × BC
Luas segitiga ABC = 1/2 × 24 cm × 18 cm
Luas segitiga ABC = 216 cm²

Karena segitiga ABC dan segitiga ACD memiliki luas yang sama, maka luas layang-layang adalah dua kali luas salah satu segitiga siku-sikunya, yaitu:

Luas layang-layang = 2 × luas segitiga ABC
Luas layang-layang = 2 × 216 cm²
Luas layang-layang = 432 cm²

Contoh 5

Jika panjang tangga adalah AC adalah x meter dan tinggi tangga adalah BC adalah y meter, berapakah luas tangga tersebut?

Jawaban:

Untuk mencari luas tangga, kita bisa membagi tangga menjadi empat buah segitiga siku-siku yang sama besar dan bentuknya, yaitu segitiga ABC, BCD, CDE, dan DEF. Kita bisa mencari luas salah satu segitiga siku-siku dengan rumus:

Luas segitiga siku-siku = 1/2 × alas × tinggi
Luas segitiga ABC = 1/2 × AC × BC
Luas segitiga ABC = 1/2 × x meter × y meter
Luas segitiga ABC = (1/2)xy meter²

Karena keempat segitiga siku-siku memiliki luas yang sama, maka luas tangga adalah empat kali luas salah satu segitiga siku-sikunya, yaitu:

Luas tangga = 4 × luas segitiga ABC
Luas tangga = 4 × (1/2)xy meter²
Luas tangga = 2xy meter²