Rumus luas tembereng lingkaran, pahami konsep dasar, unsur, contoh soal dan cara pengerjaannya

Brilio.net - Lingkaran adalah bangun datar yang terbentuk dari kumpulan titik-titik yang berjarak sama dari suatu titik pusat. Lingkaran memiliki beberapa unsur-unsur, seperti jari-jari, diameter, busur, tali busur, juring, apotema dan tembereng. Lingkaran juga memiliki rumus untuk menghitung luas dan kelilingnya.

Materi soal lingkaran ada dalam pelajaran matematika yang sudah dipelajari sejak duduk di bangku SMP. Meski kerap dianggap susah, namun jika sudah menguasai materinya jadi lebih mudah. Semakin dipelajari, materi soal lingkaran juga berkembang.

Tak hanya berkutat pada cara menghitung jari-jari dan diameter, kamu juga harus mulai mengenal luas tembereng lingkaran. Nah, kali ini brilio.net akan mengulik tentang luas tembereng lingkaran mulai dari pengertian, ciri, dan cara pengerjaan soalnya, seperti dilansir dari berbagai sumber pada Kamis (9/11).

Apa itu tembereng lingkaran?

foto: freepik.com

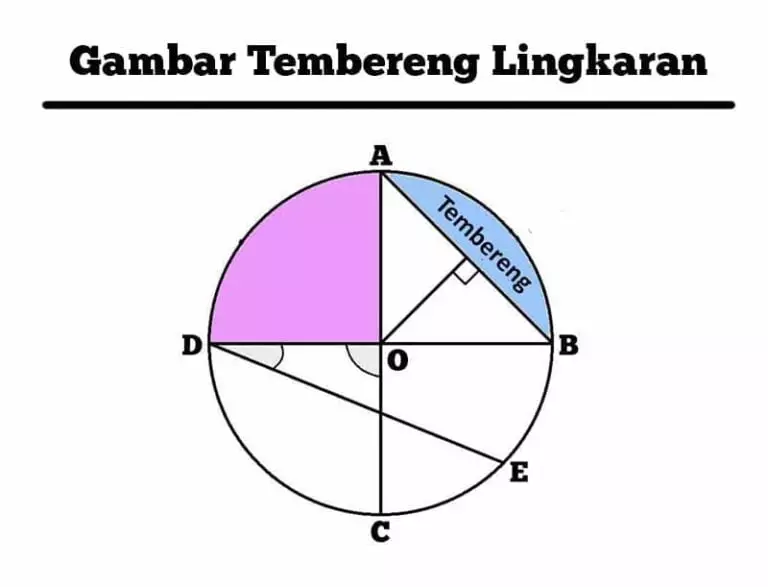
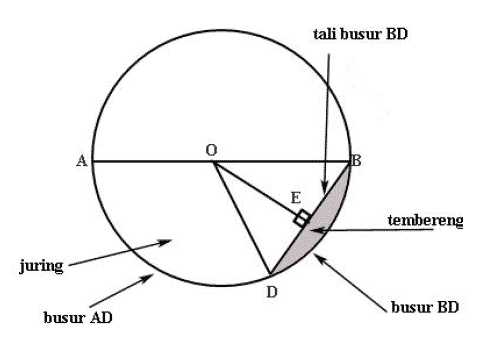
Tembereng lingkaran adalah bagian daerah dalam lingkaran yang dibatasi oleh busur dan tali busur. Busur adalah garis lengkung yang menghubungkan dua titik pada lingkaran, sedangkan tali busur adalah garis lurus yang menghubungkan dua titik tersebut. Tembereng lingkaran berada di dalam juring lingkaran, yaitu bagian daerah dalam lingkaran yang dibatasi oleh dua jari-jari dan busur.

Simak gambar berikut ini untuk memahami bagian tembereng lingkaran.

foto: Istimewa

Berdasarkan ilustrasi bentuk tembereng tersebut terdapat ciri-ciri yang bisa dipahami, yaitu:

1. Berupa daerah di dalam lingkaran.

2. Dibatasi oleh dua tali busur lingkaran dan busur lingkaran.

3. Sudut pusat lingkaran yang memuat tembereng sama dengan sudut busur lingkaran yang membatasi tembereng.

 

 

 

 

 

Rumus luas tembereng lingkaran.

foto: Istimewa

Untuk menghitung luas tembereng lingkaran, bisa menggunakan rumus luas tembereng lingkaran berikut ini:

L = r² [ (π Θ/360°) – (sin Θ/2)]

Keterangan:

L = luas tembereng lingkaran
r = jari-jari lingkaran
π = phi (22/7 atau 3,14)
Θ = sudut pusat juring lingkaran (dalam derajat)¹

Contoh soal rumus luas tembereng lingkaran.

foto: freepik.com

1. Sebuah lingkaran memiliki jari-jari 10 cm dan sudut pusat juring 60 derajat. Berapa luas tembereng lingkarannya?

Jawaban:

Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (60/360) x 22/7 x 10²
Luas juring = 11/3 x 22/7 x 100
Luas juring = 122,86 cm²

Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 10 x 10
Luas segitiga = 50 cm²

Luas tembereng = 122,86 - 50
Luas tembereng = 72,86 cm²

2. Sebuah roda sepeda berbentuk lingkaran dengan diameter 70 cm. Jika roda sepeda berputar sejauh 110 cm, berapa luas tembereng yang dibentuk oleh roda sepeda tersebut?

Jawaban:

Jari-jari lingkaran = 1/2 x diameter
Jari-jari lingkaran = 1/2 x 70
Jari-jari lingkaran = 35 cm

Panjang busur = keliling lingkaran x (θ/360)
110 = 2 x 22/7 x 35 x (θ/360)
110 = 44/7 x 35 x (θ/360)
110 x 7/44 x 1/35 x 360 = θ
θ = 57,14 derajat

Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (57,14/360) x 22/7 x 35²
Luas juring = 0,1587 x 22/7 x 1225
Luas juring = 686,25 cm²

Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 35 x 35
Luas segitiga = 612,5 cm²

Luas tembereng = 686,25 - 612,5
Luas tembereng = 73,75 cm²

3. Sebuah lingkaran memiliki jari-jari 12 cm dan tali busur 16 cm. Berapa luas tembereng yang dibentuk oleh tali busur tersebut?

Jawaban:

Sudut pusat juring = 2 x sin¹(a/2r)
Sudut pusat juring = 2 x sin¹(16/2 x 12)
Sudut pusat juring = 2 x sin¹(2/3)
Sudut pusat juring = 2 x 41,81
Sudut pusat juring = 83,62 derajat

Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (83,62/360) x 22/7 x 12²
Luas juring = 0,2323 x 22/7 x 144
Luas juring = 152,46 cm²

Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 16 x 9,6
Luas segitiga = 76,8 cm²

Luas tembereng = 152,46 - 76,8
Luas tembereng = 75,66 cm²

4. Sebuah lingkaran memiliki jari-jari 15 cm dan luas tembereng 100 cm². Berapa panjang tali busur yang membatasi tembereng tersebut?

Jawaban:

Luas tembereng = luas juring - luas segitiga
100 = (θ/360) x 22/7 x 15² - 1/2 x 15 x 15
100 = 11,25 x θ - 112,5
11,25 x θ = 212,5
θ = 18,89 derajat

Panjang tali busur = 2 x r x sin(θ/2)
Panjang tali busur = 2 x 15 x sin(18,89/2)
Panjang tali busur = 30 x sin(9,445)
Panjang tali busur = 4,92 cm

5. Sebuah lingkaran memiliki diameter 20 cm dan luas tembereng 50 cm². Berapa sudut pusat juring yang memuat tembereng tersebut?

Jawaban:

Jari-jari lingkaran = 1/2 x diameter
Jari-jari lingkaran = 1/2 x 20
Jari-jari lingkaran = 10 cm

Luas tembereng = luas juring - luas segitiga
50 = (θ/360) x 22/7 x 10² - 1/2 x 10 x 10
50 = 11,11 x θ - 50
11,11 x θ = 100
θ = 9 derajat

Berikut ini adalah tambahan 5 contoh soal rumus luas tembereng lingkaran dan jawabannya yang saya buat sendiri:

6. Sebuah lingkaran memiliki jari-jari 8 cm dan panjang tali busur 12 cm. Berapa luas tembereng yang dibentuk oleh tali busur tersebut?

Jawaban:

Untuk mengetahui luas tembereng, kita perlu mencari sudut pusat juring yang memuat tembereng tersebut. Kita bisa menggunakan rumus berikut:

Sudut pusat juring = 2 x sin¹(a/2r)

Dengan keterangan:

a = panjang tali busur
r = jari-jari lingkaran

Maka:

Sudut pusat juring = 2 x sin¹(12/2 x 8)
Sudut pusat juring = 2 x sin¹(3/4)
Sudut pusat juring = 2 x 48,59
Sudut pusat juring = 97,18 derajat

Setelah mengetahui sudut pusat juring, kita bisa mencari luas tembereng dengan rumus:

Luas tembereng = r² [ (π Θ/360°) – (sin Θ/2)]

Dengan keterangan:

r = jari-jari lingkaran
π = phi (22/7 atau 3,14)
Θ = sudut pusat juring (dalam derajat)

Maka:

Luas tembereng = 8² [ (22/7 x 97,18/360°) – (sin 97,18/2)]
Luas tembereng = 64 [ (0,2679) – (0,4695)]
Luas tembereng = 64 [ (-0,2016)]
Luas tembereng = -12,9 cm²

Namun, karena luas tidak bisa bernilai negatif, maka kita ambil nilai mutlaknya:

Luas tembereng = 12,9 cm²

7. Sebuah lingkaran memiliki diameter 10 cm dan luas tembereng 15 cm². Berapa sudut pusat juring yang memuat tembereng tersebut?

Jawaban:

Untuk mengetahui sudut pusat juring, kita perlu mencari luas juring dan luas segitiga yang membentuk tembereng tersebut. Kita bisa menggunakan rumus berikut:

Luas juring = (Θ/360°) x πr²
Luas segitiga = 1/2 x a x t

Dengan keterangan:

Θ = sudut pusat juring (dalam derajat)
π = phi (22/7 atau 3,14)
r = jari-jari lingkaran
a = panjang tali busur
t = tinggi segitiga

Karena diameter lingkaran adalah 10 cm, maka jari-jari lingkaran adalah 5 cm. Karena luas tembereng adalah 15 cm², maka kita bisa menuliskan persamaan berikut:

Luas tembereng = Luas juring - Luas segitiga
15 = (Θ/360°) x 22/7 x 5² - 1/2 x a x t

Kita perlu mencari nilai a dan t yang memenuhi persamaan tersebut. Kita bisa menggunakan teorema Pythagoras untuk mencari hubungan antara a, t, dan r. Kita bisa menuliskan persamaan berikut:

r² = (a/2)² + t²
5² = (a/2)² + t²
25 = (a/2)² + t²

Kita bisa mencoba beberapa nilai a dan t yang memenuhi persamaan tersebut. Misalnya, jika a = 8 cm, maka t = 3 cm. Jika kita substitusikan nilai a dan t tersebut ke persamaan luas tembereng, maka kita akan mendapatkan:

15 = (Θ/360°) x 22/7 x 5² - 1/2 x 8 x 3
15 = (Θ/360°) x 22/7 x 25 - 12
27 = (Θ/360°) x 22/7 x 25
27 x 360 x 7/22 x 1/25 = Θ
Θ = 94,29 derajat

Jadi, sudut pusat juring yang memuat tembereng tersebut adalah 94,29 derajat.

8. Sebuah lingkaran memiliki jari-jari 6 cm dan sudut pusat juring 120 derajat. Berapa panjang tali busur yang membatasi tembereng tersebut?

Jawaban:

Untuk mengetahui panjang tali busur, kita bisa menggunakan rumus berikut:

Panjang tali busur = 2 x r x sin(Θ/2)

Dengan keterangan:

r = jari-jari lingkaran
Θ = sudut pusat juring (dalam derajat)

Maka:

Panjang tali busur = 2 x 6 x sin(120/2)
Panjang tali busur = 12 x sin(60)
Panjang tali busur = 12 x 0,866
Panjang tali busur = 10,39 cm

Jadi, panjang tali busur yang membatasi tembereng tersebut adalah 10,39 cm.

9. Sebuah lingkaran memiliki jari-jari 9 cm dan panjang tali busur 15 cm. Berapa sudut pusat juring yang memuat tembereng tersebut?

Jawaban:

Untuk mengetahui sudut pusat juring, kita bisa menggunakan rumus berikut:

Sudut pusat juring = 2 x sin¹(a/2r)

Dengan keterangan:

a = panjang tali busur
r = jari-jari lingkaran

Maka:

Sudut pusat juring = 2 x sin¹(15/2 x 9)
Sudut pusat juring = 2 x sin¹(5/6)
Sudut pusat juring = 2 x 56,44
Sudut pusat juring = 112,88 derajat

Jadi, sudut pusat juring yang memuat tembereng tersebut adalah 112,88 derajat.