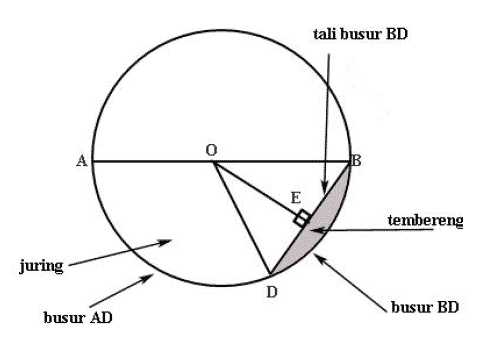
Rumus luas tembereng lingkaran.
foto: Istimewa
Untuk menghitung luas tembereng lingkaran, bisa menggunakan rumus luas tembereng lingkaran berikut ini:
L = r² [ (π Θ/360°) – (sin Θ/2)]
Keterangan:
L = luas tembereng lingkaran
r = jari-jari lingkaran
π = phi (22/7 atau 3,14)
Θ = sudut pusat juring lingkaran (dalam derajat)¹
Contoh soal rumus luas tembereng lingkaran.
foto: freepik.com
1. Sebuah lingkaran memiliki jari-jari 10 cm dan sudut pusat juring 60 derajat. Berapa luas tembereng lingkarannya?
Jawaban:
Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (60/360) x 22/7 x 10²
Luas juring = 11/3 x 22/7 x 100
Luas juring = 122,86 cm²
Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 10 x 10
Luas segitiga = 50 cm²
Luas tembereng = 122,86 - 50
Luas tembereng = 72,86 cm²
2. Sebuah roda sepeda berbentuk lingkaran dengan diameter 70 cm. Jika roda sepeda berputar sejauh 110 cm, berapa luas tembereng yang dibentuk oleh roda sepeda tersebut?
Jawaban:
Jari-jari lingkaran = 1/2 x diameter
Jari-jari lingkaran = 1/2 x 70
Jari-jari lingkaran = 35 cm
Panjang busur = keliling lingkaran x (θ/360)
110 = 2 x 22/7 x 35 x (θ/360)
110 = 44/7 x 35 x (θ/360)
110 x 7/44 x 1/35 x 360 = θ
θ = 57,14 derajat
Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (57,14/360) x 22/7 x 35²
Luas juring = 0,1587 x 22/7 x 1225
Luas juring = 686,25 cm²
Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 35 x 35
Luas segitiga = 612,5 cm²
Luas tembereng = 686,25 - 612,5
Luas tembereng = 73,75 cm²
3. Sebuah lingkaran memiliki jari-jari 12 cm dan tali busur 16 cm. Berapa luas tembereng yang dibentuk oleh tali busur tersebut?
Jawaban:
Sudut pusat juring = 2 x sin¹(a/2r)
Sudut pusat juring = 2 x sin¹(16/2 x 12)
Sudut pusat juring = 2 x sin¹(2/3)
Sudut pusat juring = 2 x 41,81
Sudut pusat juring = 83,62 derajat
Luas tembereng = luas juring - luas segitiga
Luas juring = (θ/360) x πr²
Luas juring = (83,62/360) x 22/7 x 12²
Luas juring = 0,2323 x 22/7 x 144
Luas juring = 152,46 cm²
Luas segitiga = 1/2 x a x t
Luas segitiga = 1/2 x 16 x 9,6
Luas segitiga = 76,8 cm²
Luas tembereng = 152,46 - 76,8
Luas tembereng = 75,66 cm²
4. Sebuah lingkaran memiliki jari-jari 15 cm dan luas tembereng 100 cm². Berapa panjang tali busur yang membatasi tembereng tersebut?
Jawaban:
Luas tembereng = luas juring - luas segitiga
100 = (θ/360) x 22/7 x 15² - 1/2 x 15 x 15
100 = 11,25 x θ - 112,5
11,25 x θ = 212,5
θ = 18,89 derajat
Panjang tali busur = 2 x r x sin(θ/2)
Panjang tali busur = 2 x 15 x sin(18,89/2)
Panjang tali busur = 30 x sin(9,445)
Panjang tali busur = 4,92 cm
5. Sebuah lingkaran memiliki diameter 20 cm dan luas tembereng 50 cm². Berapa sudut pusat juring yang memuat tembereng tersebut?
Jawaban:
Jari-jari lingkaran = 1/2 x diameter
Jari-jari lingkaran = 1/2 x 20
Jari-jari lingkaran = 10 cm
Luas tembereng = luas juring - luas segitiga
50 = (θ/360) x 22/7 x 10² - 1/2 x 10 x 10
50 = 11,11 x θ - 50
11,11 x θ = 100
θ = 9 derajat
Berikut ini adalah tambahan 5 contoh soal rumus luas tembereng lingkaran dan jawabannya yang saya buat sendiri:
6. Sebuah lingkaran memiliki jari-jari 8 cm dan panjang tali busur 12 cm. Berapa luas tembereng yang dibentuk oleh tali busur tersebut?
Jawaban:
Untuk mengetahui luas tembereng, kita perlu mencari sudut pusat juring yang memuat tembereng tersebut. Kita bisa menggunakan rumus berikut:
Sudut pusat juring = 2 x sin¹(a/2r)
Dengan keterangan:
a = panjang tali busur
r = jari-jari lingkaran
Maka:
Sudut pusat juring = 2 x sin¹(12/2 x 8)
Sudut pusat juring = 2 x sin¹(3/4)
Sudut pusat juring = 2 x 48,59
Sudut pusat juring = 97,18 derajat
Setelah mengetahui sudut pusat juring, kita bisa mencari luas tembereng dengan rumus:
Luas tembereng = r² [ (π Θ/360°) – (sin Θ/2)]
Dengan keterangan:
r = jari-jari lingkaran
π = phi (22/7 atau 3,14)
Θ = sudut pusat juring (dalam derajat)
Maka:
Luas tembereng = 8² [ (22/7 x 97,18/360°) – (sin 97,18/2)]
Luas tembereng = 64 [ (0,2679) – (0,4695)]
Luas tembereng = 64 [ (-0,2016)]
Luas tembereng = -12,9 cm²
Namun, karena luas tidak bisa bernilai negatif, maka kita ambil nilai mutlaknya:
Luas tembereng = 12,9 cm²
7. Sebuah lingkaran memiliki diameter 10 cm dan luas tembereng 15 cm². Berapa sudut pusat juring yang memuat tembereng tersebut?
Jawaban:
Untuk mengetahui sudut pusat juring, kita perlu mencari luas juring dan luas segitiga yang membentuk tembereng tersebut. Kita bisa menggunakan rumus berikut:
Luas juring = (Θ/360°) x πr²
Luas segitiga = 1/2 x a x t
Dengan keterangan:
Θ = sudut pusat juring (dalam derajat)
π = phi (22/7 atau 3,14)
r = jari-jari lingkaran
a = panjang tali busur
t = tinggi segitiga
Karena diameter lingkaran adalah 10 cm, maka jari-jari lingkaran adalah 5 cm. Karena luas tembereng adalah 15 cm², maka kita bisa menuliskan persamaan berikut:
Luas tembereng = Luas juring - Luas segitiga
15 = (Θ/360°) x 22/7 x 5² - 1/2 x a x t
Kita perlu mencari nilai a dan t yang memenuhi persamaan tersebut. Kita bisa menggunakan teorema Pythagoras untuk mencari hubungan antara a, t, dan r. Kita bisa menuliskan persamaan berikut:
r² = (a/2)² + t²
5² = (a/2)² + t²
25 = (a/2)² + t²
Kita bisa mencoba beberapa nilai a dan t yang memenuhi persamaan tersebut. Misalnya, jika a = 8 cm, maka t = 3 cm. Jika kita substitusikan nilai a dan t tersebut ke persamaan luas tembereng, maka kita akan mendapatkan:
15 = (Θ/360°) x 22/7 x 5² - 1/2 x 8 x 3
15 = (Θ/360°) x 22/7 x 25 - 12
27 = (Θ/360°) x 22/7 x 25
27 x 360 x 7/22 x 1/25 = Θ
Θ = 94,29 derajat
Jadi, sudut pusat juring yang memuat tembereng tersebut adalah 94,29 derajat.
8. Sebuah lingkaran memiliki jari-jari 6 cm dan sudut pusat juring 120 derajat. Berapa panjang tali busur yang membatasi tembereng tersebut?
Jawaban:
Untuk mengetahui panjang tali busur, kita bisa menggunakan rumus berikut:
Panjang tali busur = 2 x r x sin(Θ/2)
Dengan keterangan:
r = jari-jari lingkaran
Θ = sudut pusat juring (dalam derajat)
Maka:
Panjang tali busur = 2 x 6 x sin(120/2)
Panjang tali busur = 12 x sin(60)
Panjang tali busur = 12 x 0,866
Panjang tali busur = 10,39 cm
Jadi, panjang tali busur yang membatasi tembereng tersebut adalah 10,39 cm.
9. Sebuah lingkaran memiliki jari-jari 9 cm dan panjang tali busur 15 cm. Berapa sudut pusat juring yang memuat tembereng tersebut?
Jawaban:
Untuk mengetahui sudut pusat juring, kita bisa menggunakan rumus berikut:
Sudut pusat juring = 2 x sin¹(a/2r)
Dengan keterangan:
a = panjang tali busur
r = jari-jari lingkaran
Maka:
Sudut pusat juring = 2 x sin¹(15/2 x 9)
Sudut pusat juring = 2 x sin¹(5/6)
Sudut pusat juring = 2 x 56,44
Sudut pusat juring = 112,88 derajat
Jadi, sudut pusat juring yang memuat tembereng tersebut adalah 112,88 derajat.
Recommended By Editor
- Rumus persamaan garis lurus, pengertian, contoh soal serta trik mudah mengerjakannya
- Rumus limit tak hingga, lengkap dengan pengertian, fungsi dan cara mengerjakan contoh soalnya
- Rumus determinan matriks, beserta pengertian, sifat contoh soal, dan cara pengerjaannya
- Rumus suku ke-n tingkat 2, pahami konsep dasar, contoh soal dan cara pengerjaannya
- Rumus median data tunggal, lengkap dengan pengertian, penerapan, contoh soal dan pembahasannya
- Rumus prisma segi empat, lengkap dengan pengertian, ciri, dan cara menghitung