Rumus median data kelompok lengkap dengan pengertian dan cara pengerjaannya

Brilio.net - Median adalah sebuah ukuran statistik yang digunakan untuk menentukan nilai tengah dari sebuah kumpulan data yang telah diurutkan. Median merupakan nilai yang membagi data menjadi dua bagian yang sama, dengan setengah data berada di atas median dan setengahnya berada di bawahnya.

Median juga menjadi salah satu ukuran pusat yang cukup sering digunakan dalam statistik. Median tidak dipengaruhi oleh outlier atau nilai ekstrem dalam data, sehingga median dapat menjadi salah satu alternatif cara untuk menggambarkan nilai tengah yang representatif.

Dalam materi statistika, terdapat dua jenis perhitungan median, yaitu median data tunggal dan median data kelompok. Median data tunggal merupakan data sederhana yang belum dikelompokkan ke dalam kelas-kelas interval, sementara median data kelompok merupakan data berkelompok yang sudah diurutkan dari interval terkecil ke interval terbesar.

Agar kamu bisa lebih paham dan mengerti tentang median data kelompok, berikut brilio.net rangkum dari berbagai sumber tentang rumus median data kelompok lengkap dengan pengertian dan cara pengerjaannya pada Sabtu (21/10).

Pengertian media data kelompok.

foto: unsplash.com

Median data kelompok adalah jenis median yang digunakan saat data yang dimiliki telah dikelompokkan ke dalam interval atau kelas. Data kelompok sering digunakan dalam analisis statistik saat tidak memiliki akses langsung ke setiap titik data individu, tetapi hanya memiliki informasi tentang sebaran data dalam interval atau kelas.

Median data kelompok juga dinilai sebagai representasi nilai tengah dari data yang telah dikelompokkan ke dalam interval atau kelas. Perhitungan median data kelompok dapat berfungsi untuk memberikan gambaran pusat data, membuat data lebih tahan terhadap outlier atau nilai ekstrem daripada rata-rata, dan untuk memberikan gambaran yang lebih lengkap tentang distribusi data.

 

 

Rumus median data kelompok.

foto: unsplash.com

Rumus median dari data kelompok adalah sebagai berikut:

Median = L + [(n/2 - F) * w]

Di mana:

Median adalah nilai median.
L adalah batas bawah dari interval tempat median berada.
n adalah jumlah total data (jumlah frekuensi akumulasi).
F adalah jumlah frekuensi kumulatif dari interval sebelumnya.
w adalah lebar interval atau kelas.

Berikut adalah langkah-langkah untuk menghitung median dari data kelompok:

1. Identifikasi interval atau kelas tempat median berada. Biasanya ini adalah interval dengan frekuensi tengah (jika jumlah kelas adalah ganjil) atau interval antara dua interval dengan frekuensi tengah (jika jumlah kelas adalah genap).

2. Hitung jumlah kumulatif frekuensi (jumlah kumulatif) hingga mencapai atau melampaui setengah dari jumlah total data. Ini akan memberi kamu posisi median dalam data kelompok, yaitu n/2.

3. Tentukan interval tempat median berada, yaitu interval dengan frekuensi yang mencakup posisi median (n/2).

4. Hitung median menggunakan rumus di atas. Ini melibatkan batas bawah (L) dari interval median, lebar interval (w), dan perbedaan antara n/2 dan jumlah frekuensi kumulatif (F) dari interval sebelumnya.

Contoh soal dan cara pengerjaan median data kelompok.

foto: unsplash.com

1. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 5 + 12 + 18 + 7 + 3 = 45.

Median adalah nilai yang berada pada posisi ke-(n/2)
= (45/2) = 22,5. Ini berada di dalam interval "30-39".

Lebar interval (w) adalah 39 - 30 = 9.

Hitung jumlah frekuensi kumulatif (F) untuk interval sebelum "30-39":

F sebelum "30-39" = 5 (dari "10-19") + 12 (dari "20-29") = 17.

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 30 + [(22.5 - 17) * 9] = 30 + [5.5 * 9] = 30 + 49.5 = 79.5.

Jadi, median dari data ini adalah 79.5.

2. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 6 + 11 + 15 + 8 + 4 = 44.

Median adalah nilai yang berada pada posisi ke-(n/2)
= (44/2) = 22. Ini berada di dalam interval "20-29".

Lebar interval (w) = 29 - 20 = 9.

F sebelum "30-39" = 6 (dari "10-19") + 11 (dari "20-29") = 17.

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 30 + [(22 - 17) * 9] = 30 + [5 * 9] = 30 + 45 = 75

Jadi, median dari data ini adalah 75.

3. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 9 + 14 + 21 + 7 + 5 = 56.

Median adalah nilai yang berada pada posisi ke-(n/2) = (56/2) = 28. Ini berada di dalam interval "20-29".

Lebar interval (w) = 29 - 20 = 9.

F sebelum "20-29" = 9 (dari "0-9").

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 20 + [(28 - 9) * 9] = 20 + [19 * 9] = 20 + 171 = 191.

Jadi, median dari data ini adalah 191.

4. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 5 + 10 + 15 + 20 + 10 = 60.

Median adalah nilai yang berada pada posisi ke-(n/2) = (60/2) = 30. Ini berada di dalam interval "30-39".

Lebar interval (w) = 39 - 30 = 9.

F sebelum "30-39" = 5 (dari "0-9") + 10 (dari "10-19") + 15 (dari "20-29") = 30.

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 30 + [(30 - 30) * 9] = 30.

Jadi, median dari data ini adalah 30.

5. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 3 + 8 + 12 + 10 + 7 = 40.

Median adalah nilai yang berada pada posisi ke-(n/2) = (40/2) = 20. Ini berada di dalam interval "20-29".

Lebar interval (w) = 29 - 20 = 9.

F sebelum "20-29" = 3 (dari "0-9") + 8 (dari "10-19") = 11.

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 20 + [(20 - 11) * 9] = 20 + [9 * 9] = 20 + 81 = 101.

Jadi, median dari data ini adalah 101.

6. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 7 + 15 + 8 + 6 + 4 = 40.

Median adalah nilai yang berada pada posisi ke-(n/2) = (40/2) = 20. Ini berada di dalam interval "20-29".

Lebar interval (w) adalah 29 - 20 = 9.

F sebelum "20-29" = 7 (dari "10-19").

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 20 + [(20 - 7) * 9] = 20 + [13 * 9] = 20 + 117 = 137.

Jadi, median dari data ini adalah 137.

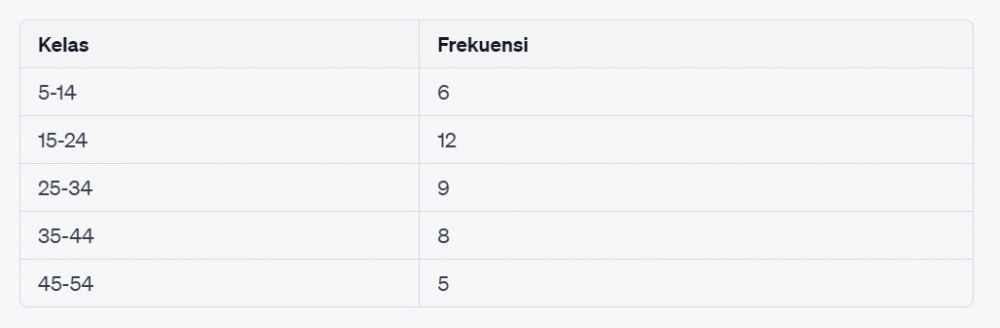
7. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 6 + 12 + 9 + 8 + 5 = 40.

Median adalah nilai yang berada pada posisi ke-(n/2) = (40/2) = 20. Ini berada di dalam interval "15-24".

Lebar interval (w) adalah 24 - 15 = 9.

F sebelum "15-24" = 6 (dari "5-14").

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 15 + [(20 - 6) * 9] = 15 + [14 * 9] = 15 + 126 = 141.

Jadi, median dari data ini adalah 141.

8. Diberikan data kelompok berikut. Hitung median dari data ini.

foto: Istimewa

Pembahasan:

Jumlah frekuensi = 3 + 8 + 10 + 5 + 4 = 30.

Median adalah nilai yang berada pada posisi ke-(n/2) = (30/2) = 15. Ini berada di dalam interval "11-15".

Lebar interval (w) adalah 15 - 11 = 4.

F sebelum "11-15" = 3 (dari "1-5") + 8 (dari "6-10") = 11.

Gunakan rumus median:
Median = L + [(n/2 - F) * w]
Median = 11 + [(15 - 11) * 4] = 11 + [4 * 4] = 11 + 16 = 27.

Jadi, median dari data ini adalah 27.