Rumus persamaan garis lurus, pengertian, contoh soal serta trik mudah mengerjakannya

Brilio.net - Materi rumus persamaan garis lurus akan diajarkan kepada siswa SMP. Ketika bab tentang aljabar sudah dilampaui, maka rumus persamaan garis lurus akan jadi materi lanjutan. Dalam materi rumus persamaan garis lurus ini, kamu akan menemukan rangkaian rumus yang berisi huruf dan angka yang seakan bertaburan.

Kalau tidak detail memahami konsep dan rumusnya, bisa jadi pelajaran rumus persamaan garis lurus ini akan pelajaran yang sangat memusingkan. Maka penting buat kamu memahami dan belajar mengerjakan soal yang menggunakan rumus persamaan garis lurus.

Dirangkum brilio.net dari berbagai sumber pada Rabu (8/11), berikut ini penjelasan tentang rumus persamaan garis lurus, pengertian, contoh soal serta trik mudah mengerjakannya.

Pengertian persamaan garis lurus

Rumus persamaan garis lurus merupakan salah satu konsep dasar dalam matematika yang digunakan untuk menggambarkan hubungan antara dua variabel dalam bentuk garis lurus di bidang kartesian.

Rumus ini memungkinkan kamu untuk memodelkan hubungan linear antara dua variabel dan menemukan titik potong garis lurus dengan sumbu x dan sumbu y. Penggunaan rumus persamaan garis lurus sangat luas, tidak hanya dalam matematika tetapi juga dalam berbagai bidang ilmu seperti fisika, ekonomi, dan teknik.

foto: ncl.ac.uk

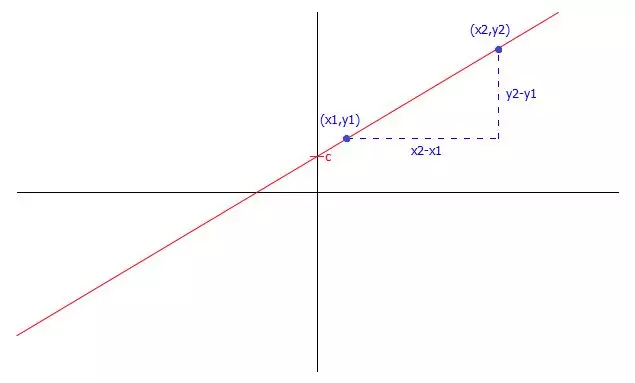
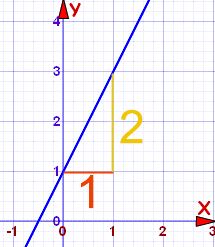
Rumus persamaan garis lurus

Adapun rumus persamaan garis lurus dalam bentuk umum adalah (y = mx + c), di mana:
- (y) adalah variabel dependen (ordinat)
- (x) adalah variabel independen (absis)
- (m) adalah gradien atau kemiringan garis
- (c) adalah intercept atau perpotongan garis dengan sumbu (y) ketika (x = 0)

Perlu diingat, Gradien (m) menunjukkan seberapa curam atau landai garis tersebut, sementara intercept (c) adalah titik di mana garis memotong sumbu (y).

Contoh soal rumus persamaan garis lurus

Contoh Soal 1:

Tentukan persamaan garis lurus dengan gradien (m = 2) dan intercept (b = 3).

Pembahasan:

Persamaan garis lurus dalam bentuk (y = mx + b), di mana (m) adalah gradien dan (b) adalah intercept. Dalam kasus ini, (m = 2) dan (b = 3), jadi persamaan garis lurusnya adalah:
y = 2x + 3

Contoh Soal 2:

Sebuah garis lurus melewati titik A(3, 5) dan memiliki gradien (m = -1). Tentukan persamaan garis lurus tersebut.

Pembahasan:
Kita sudah tahu gradiennya (m = -1) dan salah satu titik yang dilewati oleh garis A(3, 5). Untuk menentukan persamaan garis lurus, kita dapat menggunakan rumus persamaan garis lurus (y = mx + b). Gantilah (m) dengan -1 dan (x) serta (y) dengan koordinat titik A(3, 5):

5 = -1 x 3 + b

Kemudian, hitung nilai (b):
5 = -3 + b
b = 5 + 3
b = 8

Jadi, persamaan garis lurusnya adalah:
y = -x + 8

Contoh Soal 3:

Hitung gradien (m) dari garis lurus yang melewati titik P(1, 2) dan Q(5, 6).

Pembahasan:
Untuk menghitung gradien (m) dari garis lurus yang melewati dua titik P(1, 2) dan Q(5, 6), kita gunakan rumus gradien (m):

m = y2 - y1 / x2 - x1

Gantilah (x1) dengan 1, (y1) dengan 2, (x2) dengan 5, dan (y2) dengan 6:

m = (6 - 2 )/( 5 - 1)
m = 4/4
m = 1

Jadi, gradien garis lurus adalah \(m = 1\).

Contoh Soal 4:

Tentukan titik perpotongan dengan sumbu (y) (b) dari garis lurus yang memiliki persamaan (y = 4x + 7).

Pembahasan:
Persamaan garis lurus sudah diberikan dalam bentuk (y = 4x + 7). Dalam persamaan ini, (b) adalah nilai (y) ketika (x = 0). Dengan kata lain, kita sudah tahu bahwa (b = 7). Jadi, titik perpotongan dengan sumbu (y) (b) adalah 7.

Contoh Soal 5:

Jika gradien dari garis lurus adalah (m = 1/3 dan interceptnya adalah (b = 2), tentukan persamaan garis lurus tersebut.

Pembahasan:
Kita sudah memiliki nilai gradien (m = 1/3) dan intercept (b = 2). Dengan informasi ini, kita dapat langsung menyusun persamaan garis lurus:
y = 1/3 x + 2

foto: ncl.ac.uk

Trik mudah mengerjakan persamaan garis lurus

1. Perhatikan koordinat titik

Saat mengerjakan soal dengan dua titik, pastikan kamu memperhatikan koordinat kedua titik dan menggunakannya untuk menghitung gradien.

2. Perhatikan langkah-langkah

Selalu ikuti langkah-langkah yang telah ditentukan, seperti menghitung gradien terlebih dahulu dan kemudian mencari intercept.

3. Perhatikan koordinat titik perpotongan dengan sumbu (y)

Saat diberikan gradien dan titik perpotongan dengan sumbu (y), pastikan kamu mengganti nilai-nilai (m) dan (c) dengan benar pada rumus persamaan garis lurus.

foto: freepik.com

Kesimpulan

Rumus persamaan garis lurus adalah patokan dalam matematika yang penting dan sering digunakan untuk menggambarkan hubungan linear antara dua variabel dalam bentuk garis lurus.

Menghitung gradien dan intercept, serta menemukan persamaan garis dengan dua titik adalah langkah-langkah dasar yang membantu dalam menyelesaikan soal-soal terkait persamaan garis lurus.

Dengan pemahaman yang kuat tentang konsep ini dan penggunaan langkah-langkah yang tepat, penyelesaian soal-soal persamaan garis lurus dapat menjadi lebih mudah.