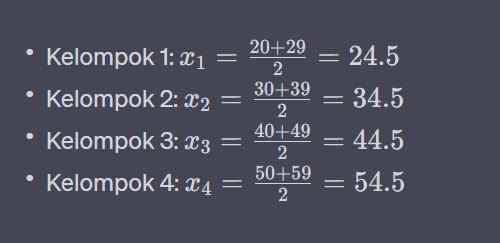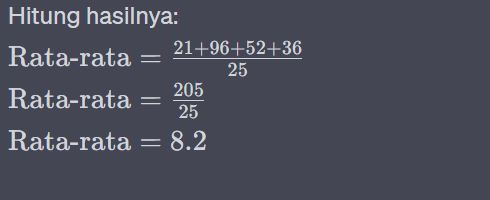Rumus rata rata data kelompok dalam statistik, pengertian, contoh soal & trik gampang mengerjakannya

Brilio.net - Rumus rata rata data kelompok, juga dikenal sebagai rata-rata berbobot dalam pelajaran statistik. Rumus ini merupakan salah satu metode untuk menghitung nilai tengah atau pusat dari sekelompok data yang telah dikelompokkan ke dalam interval atau kelas tertentu.

Rumus rata rata data kelompok sangat berguna dalam analisis statistik karena memungkinkan kamu bisa menganalisis sebuah data yang sangat besar atau terstruktur dengan lebih efisien.

Nah, khusus buat kamu yang mungkin sedang kebingungan akan apa itu rumus rata rata data kelompok, berikut ini brilio.net merangkum dari berbagai sumber pada Kamis (26/10), pengertian rata rata data kelompok, memberikan contoh soal, dan menunjukkan trik untuk menghitungnya dengan mudah. Cekidot!

Pengertian Rumus Rata Rata Data Kelompok

Rumus rata rata data kelompok dalam statistik
freepik.com

Rumus rata rata data kelompok adalah metode statistik yang digunakan untuk menemukan nilai rata-rata dari sekelompok data yang telah dikelompokkan atau diintervalkan.

Data kelompok adalah cara untuk mengorganisasi data numerik ke dalam kelompok atau interval sehingga kita dapat meringkas informasi dengan lebih efisien daripada dengan daftar panjang data tunggal.

Biasanya, rumus rata rata data kelompok digunakan ketika kamu memiliki data yang sangat luas atau beragam, seperti data dari survei, penjualan, atau hasil ujian.

Adapun rumus rata rata data kelompok tertulis seperti pada gambar berikut ini:

Rumus rata rata data kelompok dalam statistik
istimewa

Dalam rumus rata rata data kelompok ini, kamu akan mengalikan setiap titik tengah interval dengan frekuensinya. Setelah itu menjumlahkannya, untuk kemudian membaginya dengan jumlah total data dalam semua kelompok.

Contoh Soal Rumus Rata rata Data Kelompok

Sekarang, mari perhatikan contoh soal untuk lebih memahami konsep rumus rata rata data kelompok berikut ini.

Contoh Soal 1:

Sebuah toko buku ingin menghitung rata-rata usia pelanggan mereka dalam kelompok-kelompok tertentu. Mereka telah mengumpulkan data usia pelanggan dalam kelompok-kelompok sebagai berikut:

- Kelompok 1: 20-29 tahun, frekuensi (f) = 12
- Kelompok 2: 30-39 tahun, frekuensi (f) = 24
- Kelompok 3: 40-49 tahun, frekuensi (f) = 18
- Kelompok 4: 50-59 tahun, frekuensi (f) = 10

Hitunglah rata-rata usia pelanggan toko buku tersebut dalam kelompok-kelompok ini!

Pemecahan:

Langkah 1: Identifikasi titik tengah setiap kelompok. Titik tengah adalah nilai tengah dari interval.

Rumus rata rata data kelompok dalam statistik
Istimewa

Langkah 2: Gunakan rumus rata-rata data kelompok untuk menghitung rata-rata usia.

Rumus rata rata data kelompok dalam statistik
Istimewa

Jadi, rata-rata usia pelanggan toko buku tersebut dalam kelompok-kelompok ini adalah 40.125 tahun.

Contoh Soal 2: Menghitung Rata-rata Nilai Ujian Matematika

Sebuah sekolah memiliki data hasil ujian matematika siswa-siswa kelas 11 yang dikelompokkan dalam interval nilai berikut:

- Interval 50-59: Frekuensi (f) = 10 siswa
- Interval 60-69: Frekuensi (f) = 20 siswa
- Interval 70-79: Frekuensi (f) = 15 siswa
- Interval 80-89: Frekuensi (f) = 5 siswa
- Interval 90-99: Frekuensi (f) = 3 siswa

Hitung rata-rata nilai ujian matematika kelas 11!

Cara Pengerjaan:

Langkah 1: Identifikasi nilai tengah (titik tengah) dari masing-masing interval. Ini adalah nilai yang digunakan dalam perhitungan.

Rumus rata rata data kelompok dalam statistik
Istimewa

Langkah 2: Gunakan rumus rata-rata data kelompok:

Rumus rata rata data kelompok dalam statistik
Istimewa

Langkah 3: Substitusi nilai ke dalam rumus:

Rumus rata rata data kelompok dalam statistik
Istimewa

Langkah 4: Hitung hasilnya!

Rumus rata rata data kelompok dalam statistik
Istimewa

Jadi, rata-rata nilai ujian matematika kelas 11 adalah sekitar 69.01.

Contoh Soal 3: Rata-rata Penjualan Harian

Sebuah toko buku memiliki data penjualan harian dalam kelompok tertentu sebagai berikut:

Interval penjualan harian (jumlah buku terjual):

- 1-5 buku: Frekuensi (f) = 7 hari
- 6-10 buku: Frekuensi (f) = 12 hari
- 11-15 buku: Frekuensi (f) = 4 hari
- 16-20 buku: Frekuensi (f) = 2 hari

Hitung rata-rata penjualan harian toko buku!

Cara Pengerjaan:

Langkah 1: Identifikasi nilai tengah (titik tengah) dari masing-masing interval.

Rumus rata rata data kelompok dalam statistik
Istimewa

Langkah 2: Gunakan rumus rata-rata data kelompok:

Rumus rata rata data kelompok dalam statistik
Istimewa

3. Substitusi nilai ke dalam rumus:

Rumus rata rata data kelompok dalam statistik
Istimewa

4. Hitung hasilnya:

Rumus rata rata data kelompok dalam statistik
Istimewa

Jadi, rata-rata penjualan harian toko buku adalah 8.2 buku per hari.

Rumus rata rata data kelompok dalam statistik
freepik.com

Trik gampang mengerjakan soal menggunakan rumus rata rata data kelompok

Mengerjakan soal dengan rumus rata rata data kelompok bisa menjadi tugas yang membingungkan jika kamu tidak tahu cara melakukannya. Namun, ada beberapa trik yang dapat membantu kamu menghitungnya dengan lebih mudah.

1. Hitung Titik Tengah

Langkah pertama adalah menghitung titik tengah dari setiap interval atau kelompok. Hal ini dilakukan dengan menjumlahkan batas bawah dan atas interval lalu dibagi dua. Titik tengah ini adalah representasi nilai tengah dari setiap kelompok.

2. Gunakan Frekuensi

Selanjutnya, identifikasi frekuensi dari masing-masing kelompok. Ini adalah jumlah data dalam masing-masing kelompok.

3. Gunakan Rumus

Sekarang kamu siap untuk menggunakan rumus rata-rata data kelompok. Hitung perkalian dari titik tengah kelompok dengan frekuensinya untuk setiap kelompok. Kemudian, jumlahkan hasil perkalian ini.

4. Bagi dengan Jumlah Total Data

Terakhir, bagi hasil penjumlahan dengan jumlah total data dalam semua kelompok. Ini akan memberikan kamu rata-rata data kelompok.

5. Verifikasi Hasil

Pastikan bahwa hasil yang kamu dapatkan masuk akal dalam konteks masalah. Dalam contoh di atas, rata-rata usia 40.125 tahun adalah nilai yang masuk akal untuk toko buku tersebut.

Dengan menggunakan trik-trik ini, kamu dapat dengan mudah menghitung rata-rata data kelompok tanpa kesulitan yang berarti.

Kesimpulan

Rumus rata rata data kelompok adalah metode statistik yang berguna untuk menghitung rata-rata dari sekelompok data yang telah dikelompokkan ke dalam interval atau kelompok.

Hal ini sangat berguna saat kamu memiliki data yang sangat luas atau terstruktur. Pasalnya, cara tersebut memungkinkan kamu bisa meringkas informasi dengan lebih efisien.

Untuk menghitung rata-rata data kelompok, kita perlu mengidentifikasi titik tengah dari masing-masing kelompok, menghitung frekuensi dari setiap kelompok, dan menggunakan rumus yang tepat. Dengan memahami konsep ini dan mengikuti langkah-langkah yang tepat, kamu dapat dengan mudah menghitung rata-rata data kelompok dalam berbagai situasi statistik.