Rumus rotasi transformasi geometri, beserta pengertian, sifat, dan cara pengerjaannya

Brilio.net - Transformasi geometri merupakan perubahan dalam bentuk, ukuran, atau posisi objek geometris dalam ruang dua-atau tiga-dimensi. Transformasi ini digunakan dalam matematika dan ilmu geometri untuk menggambarkan perubahan pada benda-benda geometris tanpa mengubah properti dasar mereka seperti keliling, sudut, atau hubungan relatif antara titik-titik.

Nah, transformasi geometri terdiri dari beberapa jenis seperti translasi, rotasi, refleksi, dilatasi atau scaling, dan shearing. Pada artikel kali ini, brilio.net memberikan ulasan lengkap tentang rumus rotasi transformasi geometri. Rotasi transformasi geometri merupakan perubahan arah atau sudut objek, tetapi tidak mengubah ukuran, bentuk, atau struktur objek tersebut.

Supaya makin memahami tentang rumus rotasi transformasi geometri ini, berikut brilio.net berikan ulasan lengkapnya. Dirangkum dari berbagai sumber pada Kamis (19/10) Yuk simak dibawah ini!

Pengertian rotasi transformasi geometri.

foto: Istimewa

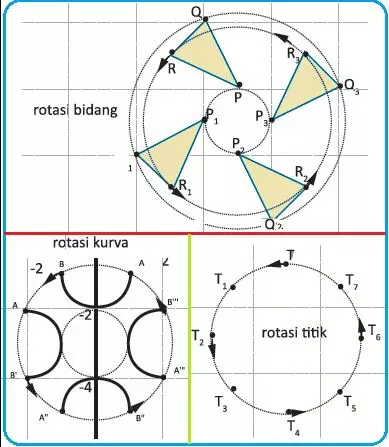
Rotasi adalah salah satu jenis transformasi geometri yang merujuk pada perubahan posisi atau orientasi objek geometris dengan memutarnya sekitar titik tertentu, yang disebut sebagai pusat rotasi. Rotasi mengubah arah atau sudut objek, tetapi tidak mengubah ukuran, bentuk, atau struktur objek tersebut.

Dalam konteks rotasi, beberapa konsep penting yang perlu dipahami adalah:

1. Pusat Rotasi (Origin): Ini adalah titik atau koordinat tempat objek berputar. Semua titik pada objek akan berputar sekitar pusat rotasi ini.

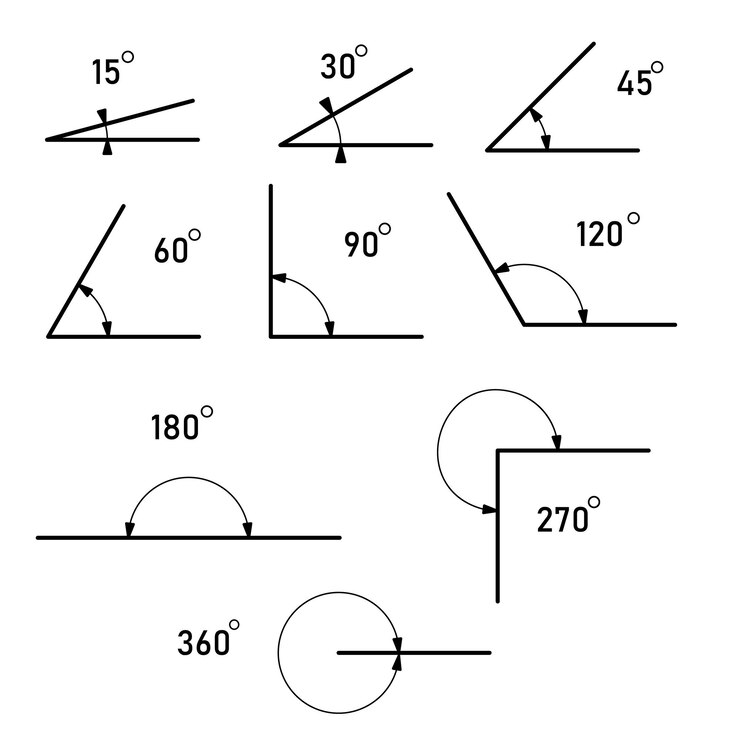
2. Sudut Rotasi: Sudut rotasi mengukur seberapa jauh objek diputar dalam derajat (untuk objek dua dimensi) atau sudut radian (untuk objek tiga dimensi). Jika objek diputar searah jarum jam, sudut rotasi positif, sedangkan jika diputar berlawanan arah jarum jam, sudut rotasi negatif.

3. Arah Rotasi: Objek dapat diputar searah jarum jam atau berlawanan arah jarum jam sekitar pusat rotasi. Arah rotasi ini ditentukan oleh tangan yang digunakan, misalnya, arah rotasi dengan jari telunjuk tangan kanan adalah searah jarum jam.

Rotasi dalam dua dimensi dapat diilustrasikan dengan contoh sederhana seperti mengatur perubahan orientasi jarum jam atau arah berlawanan jarum jam, sedangkan rotasi dalam tiga dimensi melibatkan perubahan orientasi objek di sekitar tiga sumbu koordinat.

Rotasi adalah konsep penting dalam berbagai bidang, termasuk matematika, ilmu komputer, fisika, dan ilmu teknik. Misalnya, dalam grafika komputer, rotasi digunakan untuk menganimasikan objek dan perubahan orientasi, sedangkan dalam mekanika, rotasi memainkan peran penting dalam menganalisis gerakan benda putar seperti roda atau rotor.

Sifat rumus rotasi transformasi geometri.

foto: Istimewa

Transformasi geometri memiliki beberapa sifat, antara lain:

1. Transformasi geometri dapat mengubah bentuk dan ukuran objek, tetapi tidak mengubah sifat-sifat geometrisnya, seperti sudut, jarak, dan kesejajaran.

2. Transformasi geometri dapat digabungkan untuk menghasilkan transformasi baru. Misalnya, translasi dan refleksi dapat digabungkan menjadi transformasi geser.

3. Transformasi geometri dapat direpresentasikan dengan menggunakan matriks. Matriks dapat digunakan untuk menghitung koordinat objek asli dan objek bayangan setelah transformasi.

 

Rumus rotasi transformasi geometri.

foto: freepik.com

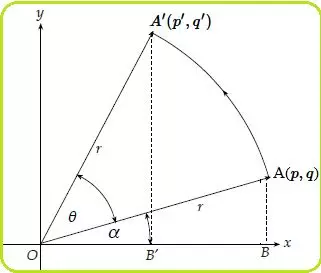
Rotasi adalah perputaran suatu objek sebesar sudut tertentu terhadap suatu titik pusat. Rotasi tidak mengubah bentuk dan ukuran objek, hanya mengubah arahnya. Contohnya, saat kita memutar kunci di gembok, kunci tersebut mengalami rotasi. Rumus rotasi untuk titik (x,y) yang diputar sebesar θ derajat berlawanan arah jarum jam terhadap titik pusat (0,0) atau (a,b) adalah:

x′ = xcosθ − ysinθ

y′ = xsinθ + ycosθ

Keterangan:

x′ dan y′ adalah koordinat titik bayangan setelah rotasi

x dan y adalah koordinat titik awal sebelum rotasi

θ adalah sudut rotasi yang diukur berlawanan arah jarum jam
Titik pusat rotasi adalah (0,0)

Rumus ini berlaku jika titik pusat rotasi adalah (0,0).

Jika titik pusat rotasi adalah (a,b), maka rumusnya menjadi:

x′ = (x − a)cosθ − (y − b)sinθ + a

y′ = (x − a)sinθ + (y − b)cosθ + b

Contoh soal rotasi transformasi geometri.

foto: freepik.com

Soal 1

Titik A(2,3) diputar sebesar 180 derajat berlawanan arah jarum jam terhadap titik pusat O(0,0). Tentukan koordinat titik bayangan A’!

Jawab:

Rumus rotasi terhadap titik pusat (0,0) adalah:

x′ = xcosθ − ysinθ

y′ = xsinθ + ycosθ

Keterangan:

(x′,y′) adalah koordinat titik bayangan setelah rotasi

(x,y) adalah koordinat titik asal sebelum rotasi

θ adalah sudut rotasi yang diukur berlawanan arah jarum jam

Substitusi nilai-nilai yang diketahui ke dalam rumus:

x′ = 2cos180° − 3sin180°

y′ = 2sin180° + 3cos180°

Gunakan kalkulator atau tabel trigonometri untuk mencari nilai cosinus dan sinus:

x′n=n2(−1) − 3(0)

y′ = 2(0) + 3(−1)

Sederhanakan hasilnya:

x′ = −2

y′ = −3

Jadi, koordinat titik bayangan A’ adalah (−2,−3).

Soal 2

Titik B(-4,5) diputar sebesar 90 derajat searah jarum jam terhadap titik pusat P(1,2). Tentukan koordinat titik bayangan B’!

Jawab:

Rumus rotasi terhadap titik pusat (a,b) adalah:

x′ =( x − a)cosθ − (y − b)sinθ + a

y′ = (x − a)sinθ + (y − b)cosθ + b

Keterangan:

(x′,y′) adalah koordinat titik bayangan setelah rotasi

(x,y) adalah koordinat titik asal sebelum rotasi

θ adalah sudut rotasi yang diukur berlawanan arah jarum jam

(a,b) adalah koordinat titik pusat rotasi

Substitusi nilai-nilai yang diketahui ke dalam rumus:

x′ = (−4 −1)cos(−90°) − (5−2)sin(−90°) + 1

y′ = (−4 −1)sin(−90°) + (5 − 2)cos(−90°) + 2

Gunakan kalkulator atau tabel trigonometri untuk mencari nilai cosinus dan sinus:

x′ = (−5)(0) − (3)(−1) + 1

y′ =( −5)(−1) + (3)(0) + 2

Sederhanakan hasilnya:

x′ = 4

y′ = 7

Jadi, koordinat titik bayangan B’ adalah (4,7).

Soal 3

Titik C(3,-2) diputar sebesar -45 derajat berlawanan arah jarum jam terhadap titik pusat O(0,0). Tentukan koordinat titik bayangan C’!

Jawab:

Rumus rotasi terhadap titik pusat (0,0) adalah:
x′ =xcosθ − ysinθ

y′ = xsinθ + ycosθ

Keterangan:

(x′,y′) adalah koordinat titik bayangan setelah rotasi

(x,y) adalah koordinat titik asal sebelum rotasi

θ adalah sudut rotasi yang diukur berlawanan arah jarum jam

Substitusi nilai-nilai yang diketahui ke dalam rumus:

x′ = 3cos(−45°) − (−2)sin(−45°)

y′ = 3sin(−45°) + (−2)cos(−45°)

Gunakan kalkulator atau tabel trigonometri untuk mencari nilai cosinus dan sinus:

x′ = 3 (√2/2) - (-2)(√2/2)

y′ = 3(-√2/2) + (-2)(√2/2)

Sederhanakan hasilnya:

x′ = 5√2/2

y′ = 5√2/2

Jadi, koordinat titik bayangan C’ adalah (5√2/2, - 5√2/2)

Soal 4

Titik D(1,4) diputar sebesar 60 derajat searah jarum jam terhadap titik pusat Q(-1,1). Tentukan koordinat titik bayangan D’!

Jawab:

Rumus rotasi terhadap titik pusat (a,b) adalah:

x′ = (x − a)cosθ − (y − b)sinθ + a

y′ = (x − a)sinθ + (y − b)cosθ + b

Keterangan:

(x′,y′) adalah koordinat titik bayangan setelah rotasi

(x,y) adalah koordinat titik asal sebelum rotasi

θ adalah sudut rotasi yang diukur berlawanan arah jarum jam

(a,b) adalah koordinat titik pusat rotasi

Substitusi nilai-nilai yang diketahui ke dalam rumus:

x′ = (1 − (−1))cos(60°) − (4 − 1)sin(60°) + (−1)

y′ = (1 − (−1))sin(60°) + (4 − 1)cos(60°) + 1

Gunakan kalkulator atau tabel trigonometri untuk mencari nilai cosinus dan sinus:

x′ = (2)(1/2) - (3)(√3/2) + (-1)

y′ = (2)(√3/2) + 3 (1/2) + 1

Sederhanakan hasilnya:

x′ = -√3/2 - 1

y′ = (√3 + 3

Jadi, koordinat titik bayangan D’ adalah (-√3/2 - 1, √3 + 3).