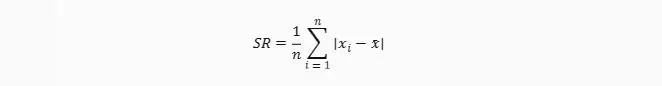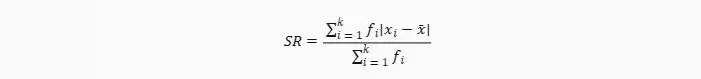Rumus simpangan rata-rata, beserta pengertian dan contoh soalnya

Brilio.net - Simpangan rata-rata menjadi salah satu pembahasan sub statistik yang menarik untuk dipelajari. Materi statistik ini penting dipelajari karena bisa digunakan untuk menganalisis seberapa besar selisih atau penyimpangan dan area persebaran data-data statistik.

Secara sederhana, simpangan rata-rata dapat dipahami sebagai ukuran penyebaran data yang menghitung rata-rata jarak antara setiap nilai data dengan nilai rata-ratanya. Simpangan rata-rata juga disebut sebagai deviasi mean. Rumus simpangan rata-rata digunakan untuk mengetahui seberapa jauh nilai menyimpang dari rata-ratanya dan bagaimana persebaran data statistik.

Dengan menggunakan rumus simpangan rata-rata, kamu bisa membagikan mana data yang penyebaran rendah dan mana yang tinggi. Apabila data yang penyebaran rendah berarti nilai-nilainya dekat dengan rata-ratanya, sedangkan data yang penyebarannya tinggi berarti nilai-nilainya jauh dari rata-ratanya.

Selain itu, rumus simpangan rata-rata juga dapat digunakan untuk membandingkan dua atau lebih kelompok data yang memiliki rata-rata sama. Adapun rumus simpangan rata-rata terdiri dari dua jenis, yaitu untuk data tunggal dan data kelompok. Kedua pembagian rumus simpangan rata-rata penting untuk dipelajari.

Yuk sama-sama simak ulasan lengkap rumus simpangan rata-rata mulai dari pengertian, contoh soal dan pembahasannya. Brilio.net merangkum dari berbagai sumber, Jumat (13/10).

Pengertian dan rumus simpangan rata-rata.

foto: freepik.com

Simpangan rata-rata, yang juga dikenal sebagai simpangan absolut rata-rata, adalah ukuran statistik yang digunakan untuk mengukur sejauh mana nilai-nilai dalam suatu kumpulan data tersebar dari nilai rata-rata (mean) kumpulan data tersebut. Simpangan rata-rata memberikan gambaran tentang seberapa jauh titik data individual dalam kumpulan data berbeda dari nilai rata-rata, dan mengukur besaran absolut (positif) dari perbedaan ini.

Simpangan rata-rata dihitung dengan cara berikut:

1. Selisihkan setiap nilai data dalam kumpulan data dengan nilai rata-rata kumpulan data tersebut.

2. Ambil nilai absolut (nilai positif) dari selisih-selisih tersebut.

3. Jumlahkan semua nilai-nilai absolut yang dihasilkan dalam langkah kedua.

4. Bagi jumlah nilai absolut tersebut dengan jumlah total data dalam kumpulan data untuk mendapatkan simpangan rata-rata.

Adapun rumus menghitung simpangan rata-rata terdapat dua rumus yaitu data tunggal dan data berkelompok. Berikut adalah rumusnya:

- Untuk data tunggal, simpangan rata-rata adalah jumlah seluruh nilai mutlak selisih antara setiap nilai data dengan rata-ratanya, dibagi dengan banyaknya data. Rumusnya adalah:

foto: Istimewa

- Untuk data berkelompok, simpangan rata-rata adalah jumlah seluruh perkalian antara frekuensi dan nilai mutlak selisih antara nilai tengah kelas dengan rata-ratanya, dibagi dengan jumlah seluruh frekuensi. Rumusnya adalah:

foto: Istimewa

Keterangan:

- SR adalah simpangan rata-rata
- n adalah banyaknya data
- xi adalah nilai data ke-i
- x adalah rata-rata data
- k adalah banyaknya kelas
- fi adalah frekuensi kelas ke-i