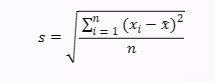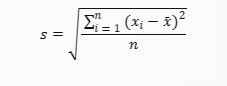Rumus standar deviasi, lengkap dengan pengertian, fungsi, contoh soal dan pembahasannya

Brilio.net - Istilah standar deviasi sudah nggak asing lagi bagi mahasiswa ekonomi maupun akuntansi. Pasalnya rumus standar deviasi berkaitan erat dengan data statistik yang membantu kamu menganalisis maupun menguji suatu data. Lantas, apa itu standar deviasi?

Standar deviasi adalah suatu nilai yang menunjukkan tingkat penyebaran terhadap nilai rata-rata data tersebut. Standar deviasi digunakan untuk menunjukkan seberapa dekat atau jauh data individu dari nilai rata-rata (mean) data tersebut.

Semakin kecil standar deviasi, berarti data lebih konsisten atau homogen. Semakin besar standar deviasi, berarti data lebih bervariasi atau heterogen. Untuk menghitung standar deviasi menggunakan rumus tersendiri.

Nah, supaya kamu lebih paham tentang rumus standar deviasi, yuk simak ulasan lengkapnya mulai dari pengertian, fungsi dan contoh serta pembahasan yang mudah dipahami, seperti yang telah brilio.net himpun dari berbagai sumber pada Jumat (13/10).

Pengertian standar deviasi.

Rumus standar deviasi
freepik.com

Standar deviasi adalah ukuran statistik yang digunakan untuk mengetahui seberapa besar variasi atau penyebaran data dalam suatu sampel atau populasi. Standar deviasi menunjukkan seberapa dekat atau jauh data individu dari nilai rata-rata (mean) data tersebut. Semakin kecil standar deviasi, berarti data lebih konsisten atau homogen. Semakin besar standar deviasi, berarti data lebih bervariasi atau heterogen.

Adapun pengertian penting dalam standar deviasi, yaitu:

1. Rata-rata (Mean)

Nilai rata-rata adalah jumlah total dari semua data dibagi oleh jumlah data. Standar deviasi mengukur sejauh mana data-data ini berbeda dari rata-rata.

2. Dispersi

Standar deviasi menggambarkan seberapa merata atau tidak meratanya data di sekitar rata-rata. Semakin tinggi standar deviasi, semakin besar variasi atau penyebaran data. Sebaliknya, semakin rendah standar deviasi, semakin dekat nilai-nilai data dengan rata-rata.

3. Pengukuran ketidakpastian

Standar deviasi juga digunakan untuk mengukur tingkat ketidakpastian dalam data statistik. Semakin besar standar deviasi, semakin tidak pasti kita dalam memprediksi nilai spesifik dalam kumpulan data.

4. Interpretasi

Standar deviasi dapat digunakan untuk membandingkan dua atau lebih kelompok data. Kelompok data dengan standar deviasi yang lebih rendah cenderung lebih homogen daripada kelompok data dengan standar deviasi yang lebih tinggi.

5. Simbol

Simbol standar deviasi populasi adalah σ (sigma), sedangkan simbol standar deviasi sampel adalah s. Standar deviasi populasi digunakan ketika seluruh populasi diamati, sedangkan standar deviasi sampel digunakan ketika hanya sebagian kecil dari populasi yang diamati.

Standar deviasi adalah alat yang penting dalam analisis statistik, dan informasi yang diberikannya membantu kamu memahami karakteristik dan variasi dalam data. Standar deviasi digunakan dalam berbagai bidang, termasuk statistik, ilmu sosial, ilmu ekonomi, ilmu alam, dan ilmu keuangan, untuk mengevaluasi dan memahami data yang dikumpulkan.

 

 

Rumus standar deviasi
freepik.com

Rumus standar deviasi digunakan untuk mengukur sejauh mana data tersebar dari nilai rata-rata (mean) dalam sebuah kumpulan data. Standar deviasi merupakan ukuran dispersi yang penting dalam statistik. Standar deviasi dapat dihitung dengan rumus:

 

 

Rumus standar deviasi
Istimewa

Keterangan:
- s adalah standar deviasi
- xi adalah data ke-i-
- x adalah nilai rata-rata (mean) data
- n adalah jumlah data

Rumus Standar Deviasi Populasi (σ):

Rumus standar deviasi
Istimewa

Rumus Standar Deviasi Sampel (s):

Rumus standar deviasi
Istimewa

Keterangan:

- σ adalah standar deviasi populasi.
- s adalah standar deviasi sampel.
- x adalah setiap nilai dalam kumpulan data.
- μ adalah rata-rata (mean) dari populasi.
- x adalah rata-rata (mean) dari sampel.
- Σ menunjukkan penjumlahan (Σ(x) berarti jumlah semua nilai dalam kumpulan data).
- N adalah jumlah total data dalam populasi.
- n adalah jumlah sampel dalam data sampel.

Perbedaan antara rumus standar deviasi populasi dan sampel terletak pada pembaginya: standar deviasi populasi dibagi dengan jumlah total data dalam populasi (N), sedangkan standar deviasi sampel dibagi dengan jumlah sampel dikurangi satu (n-1). Hal ini disebabkan oleh konsep derajat kebebasan dalam statistik.

Standar deviasi digunakan untuk mengukur tingkat variasi atau dispersi dalam data. Semakin tinggi standar deviasi, semakin besar variasi dalam data. Sebaliknya, semakin rendah standar deviasi, semakin dekat nilai-nilai dalam data dengan rata-rata. Standar deviasi adalah alat yang berguna untuk menganalisis distribusi data dan memahami sejauh mana data tersebut tersebar.

Fungsi standar deviasi.

Rumus standar deviasi
freepik.com

Standar deviasi memiliki beberapa fungsi penting dalam statistik dan analisis data. Berikut adalah beberapa fungsi utama dari standar deviasi:

1. Mengukur Variabilitas Data

Fungsi utama dari standar deviasi adalah mengukur sejauh mana nilai-nilai dalam suatu kumpulan data tersebar atau bervariasi dari nilai rata-ratanya. Semakin besar standar deviasi, semakin besar variasi dalam data. Ini membantu kita memahami sejauh mana data berbeda dari rata-rata dan seberapa heterogen distribusi data tersebut.

2. Pembandingan Data

Standar deviasi memungkinkan perbandingan antara berbagai kelompok data. Dengan membandingkan standar deviasi dari dua atau lebih kelompok data, dengan begitu kamu dapat menentukan kelompok mana yang lebih konsisten atau homogen. Kelompok dengan standar deviasi yang lebih rendah cenderung lebih konsisten.

3. Mengidentifikasi Outlier

Standar deviasi dapat membantu mengidentifikasi data outlier atau data yang sangat berbeda dari yang lain dalam kumpulan data. Data outlier cenderung memiliki deviasi yang tinggi dari rata-rata, dan ini dapat memberikan petunjuk tentang data yang perlu diperhatikan lebih lanjut.

4. Mengukur Ketidakpastian

Standar deviasi juga digunakan untuk mengukur tingkat ketidakpastian dalam data statistik. Semakin tinggi standar deviasi, semakin tidak pasti kita dalam memprediksi nilai spesifik dalam kumpulan data.

5. Evaluasi Distribusi Data

Standar deviasi digunakan untuk mengidentifikasi karakteristik distribusi data. Distribusi yang memiliki standar deviasi rendah menunjukkan bahwa data-data cenderung berkumpul dekat rata-rata, sedangkan distribusi dengan standar deviasi tinggi menunjukkan bahwa data-data cenderung tersebar lebih jauh dari rata-rata.

6. Penentuan Signifikansi Statistik

Standar deviasi digunakan dalam berbagai uji statistik, termasuk uji hipotesis. Ini membantu peneliti dan analis dalam menentukan apakah perbedaan antara dua kelompok data atau hasil eksperimen signifikan atau hanya hasil dari kebetulan.

7. Pemahaman Karakteristik Data

Standar deviasi adalah alat penting dalam pemahaman karakteristik data. Dengan memahami sejauh mana data terdispersi, analis dapat membuat prediksi yang lebih akurat, mengidentifikasi pola, dan membuat keputusan yang lebih baik dalam berbagai konteks, termasuk bisnis, ilmu sosial, dan ilmu alam.

Dengan demikian, standar deviasi adalah alat yang penting dalam statistik yang membantu kita memahami variasi dan karakteristik data. Ini digunakan dalam berbagai aplikasi statistik dan analisis data untuk mengambil keputusan dan membuat kesimpulan yang lebih baik berdasarkan data yang diamati.

Contoh soal dan pembahasan seputar rumus standar deviasi.

Rumus standar deviasi
freepik.com

1. Data nilai ulangan matematika kelas XI adalah:

80, 85, 90, 95, 100, 105, 110

Hitunglah standar deviasi data tersebut dengan menggunakan rumus:

Rumus standar deviasi
Istimewa

Jawaban:

Rumus standar deviasi
Istimewa

Jadi, standar deviasi data nilai ulangan matematika kelas XI adalah 10.

2. Data berat badan (kg) siswa kelas XII adalah:
50, 55, 60, 65, 70, 75, 80

Hitunglah standar deviasi data tersebut dengan menggunakan rumus:

Rumus standar deviasi
Istimewa

Jawaban:

Rumus standar deviasi
Istimewa

Jadi, standar deviasi data berat badan siswa kelas XII adalah 10 kg.

3. Sebuah toko buku mencatat penjualan harian dalam lima hari terakhir sebagai berikut: 20, 25, 18, 22, dan 27 buku. Hitunglah standar deviasi dari penjualan harian tersebut.

Jawaban:

Langkah 1: Hitung rata-rata (mean) penjualan harian.

Rata-Rata = 20 + 25 + 18 + 22 + 27/5 = 112/5 = 22,4

Langkah 2: Hitung deviasi dari setiap nilai terhadap rata-rata dan kemudian kuadrat deviasi tersebut.

(20−22.4)² = 6.76
(25−22.4)² = 6.76
(18−22.4)² = 19.36
(22−22.4)² = 0.16
(27−22.4)² = 20.25

Langkah 3: Jumlahkan kuadrat deviasi dan bagi hasilnya dengan jumlah data minus satu.

Rumus standar deviasi
Istimewa

Jadi, standar deviasi penjualan harian adalah sekitar 3.65 buku.

4. Sebuah tim sepak bola mencatat jumlah gol yang dicetak dalam 8 pertandingan terakhir mereka: 2, 3, 1, 0, 4, 2, 3, dan 1 gol. Hitunglah standar deviasi jumlah gol yang dicetak.

Jawaban:

Langkah 1: Hitung rata-rata (mean) jumlah gol yang dicetak.

Rumus standar deviasi
Istimewa

Langkah 2: Hitung deviasi dari setiap jumlah gol terhadap rata-rata dan kemudian kuadrat deviasi tersebut.

(2−2)² = 0
(3−2)² = 1
(1−2)² = 1
(0−2)² = 4
(4−2)² = 4
(2−2)² = 0
(3−2)² = 1
(1−2)² = 1

Langkah 3: Jumlahkan kuadrat deviasi dan bagi hasilnya dengan jumlah data minus satu.

Rumus standar deviasi
Istimewa

Jadi, Standar deviasi jumlah gol yang dicetak adalah sekitar 1.30 gol.