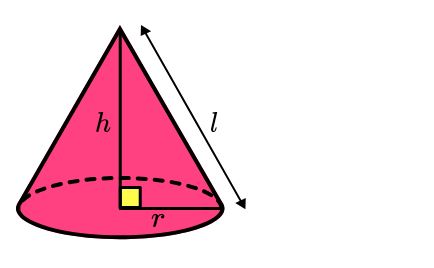
Contoh Soal Rumus Tinggi Kerucut beserta Pembahasannya

1. Sebuah kerucut memiliki jari-jari lingkaran dasar sepanjang 8 cm dan garis lengkung sepanjang 10 cm. Hitunglah tinggi kerucut tersebut.

Pembahasan:
Gunakan rumus tinggi kerucut:
h = l - r
h = 10 - 8
h = 100 - 64
h = 36
h = 6 cm

2. Sebuah kerucut memiliki tinggi 12 cm dan jari-jari lingkaran dasar 5 cm. Tentukan panjang garis lengkungnya.

Pembahasan:
Gunakan rumus tinggi kerucut:
l = r + h
l = 5 + 12
l = 25 + 144
l = 169
l = 13 cm

3. Sebuah kerucut memiliki tinggi 15 cm dan garis lengkung 17 cm. Hitunglah jari-jari lingkaran dasarnya.

Pembahasan:
Gunakan rumus tinggi kerucut:
r = l - h
r = 17 - 15
r = 289 - 225
r = 64
r = 8 cm

4. Jika tinggi sebuah kerucut 9 cm dan jari-jari lingkaran dasarnya 6 cm, berapakah panjang garis lengkungnya?

Pembahasan:
Gunakan rumus tinggi kerucut:
l = r + h
l = 6 + 9
l = 36 + 81
l = 117
l = 10.82 cm

Rumus tinggi kerucut Berbagai sumber

foto: thirdspacelearning.com

5. Sebuah kerucut memiliki tinggi 10 cm dan panjang garis lengkungnya 13 cm. Tentukan jari-jari lingkaran dasarnya.

Pembahasan:
Gunakan rumus tinggi kerucut:
r = l - h

r = 13 - 10
r = 169 - 100
r = 69
r = 8.3 cm

6. Sebuah kerucut memiliki jari-jari lingkaran dasar sepanjang 3 cm dan tinggi 16 cm. Hitunglah panjang garis lengkung.

Pembahasan:
Gunakan rumus tinggi kerucut:
l = r + h
l = 3 + 16
l = 9 + 256
l = 265
l = 16.28 cm

7. Sebuah kerucut memiliki panjang garis lengkung sepanjang 20 cm dan tinggi 15 cm. Berapakah jari-jari lingkaran dasarnya?

Pembahasan:
Gunakan rumus tinggi kerucut:
r = l - h
r = 20 - 15
r = 400 - 225
r = 175
r = 13.23 cm